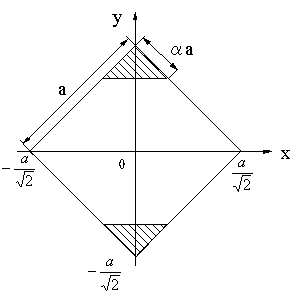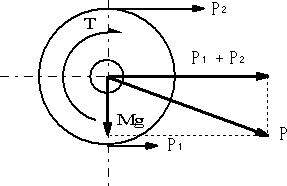| 【問題3】 |
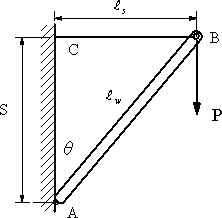
図3のように部材ABの中心に荷重Pが作用しているとき、 部材BCに作用する荷重Tを求める。
|
|
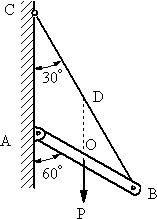
図3
|
|
【解答例】
|
| 【問題4】 |
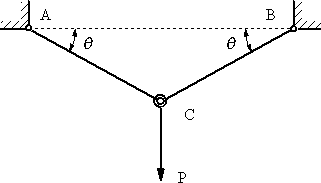
5本の部材からなる図4のトラス、接点B, Cで支持され、D点に荷重Pが作用している。各部材に作用する内力と支点の反力を求める。 |
|
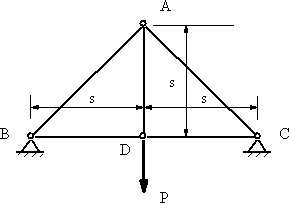
図4
|
| |
【解答例】 |
| |
|
| 【問題5】 |
長さlの銅管を鋼製のボルトが貫通して、左端のナットが温度T1で銅管にすき間無く接触している。その後、ナットをn回転して銅管を締める。
|
| (1). |
この時、ボルトと銅管に生ずる応力σsとσcを求める。ただし、ボルトのピッチs
mm ボルトと銅管のヤング係数Es Ecとする。ボルトと銅管の断面積As、Ac |
| (2). |
温度がΔT上昇したとき、ボルトと銅管に生ずる応力σsとσcを求める。ただし、ボルトと銅管の線膨張係数αs,
αcとする。 |
|
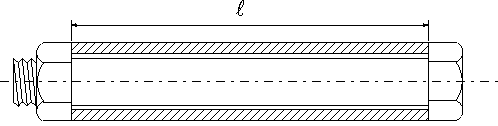
図5
|
|
【解答例】
|
| 【問題6】 |
図6のように均一な板厚の鋼製の中空円筒の中にコンクリートを充填する。剛体の板を上に載せて荷重Pを負荷したとき、各々の材料に生ずる応力と円筒の圧縮量を求める。また、鋼製の中空円筒とコンクリートを複合させたユング率Eを求める。
鋼製の中空円筒、コンクリートの両材ともフックの法則が成り立ち、ヤング率をそれぞれ、Es,Ec、断面積As、Acとし、円筒の長さをlとする。 |
|
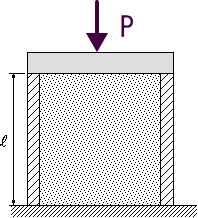
図6 ヤング率をそれぞれ、Es,Ec、断面積As、Ac
|
|
【解答例】
|
| 【問題7】 |
両端を剛体の壁によって固定された、長さl、 断面積A、ヤング係数Eの一様な円形断面の鋼材の棒がC点で荷重Pを受けるとき、剛体壁から受ける力RA,RBとC点の移動量δを求める。 |
|
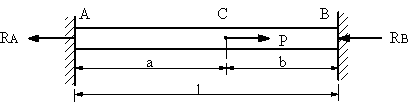
図7
|
|
【解答例】
|
| 【問題8】 |
直径d、長さlの鋼材の丸棒が、引張荷重Pをうけて、ポアソン効果により、直径がΔdだけ減少した。Δdを求めよ。鋼材のヤング係数をE、ポアソン比νとする。
次に、P=20kN=2×104N lw=5m=5×103 mm , l=3m=3×103 mm , d=25 mm=2.5×10mm, E=20.6×104MPa、ν=0.3のとき、Δdを:計算する。 |
|
【解答例】
|
| 【問題9】 |
図のはりの場合、せん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。 |
|
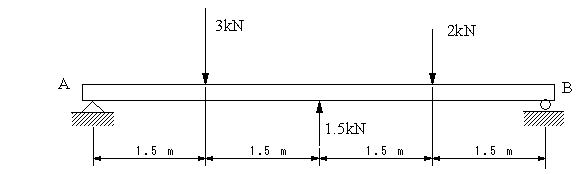 |
|
【解答例】
|
| 【問題10】 |
図のI型鋼の断面2次モーメントと断面係数を求める(b1>b2)。 |
|
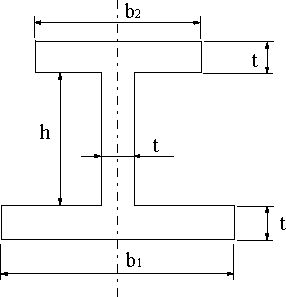 |
|
【解答例】
|
| 【問題11】 |
図の場合に、せん断力Vx、曲げモーメントMx、たわみyを求める。はりの断面二次モーメントI,
ヤング係数Eとする。 |
|
|
| 【問題12】 |
図の半径rの半円形状の断面二次モーメントを計算する。 |
|
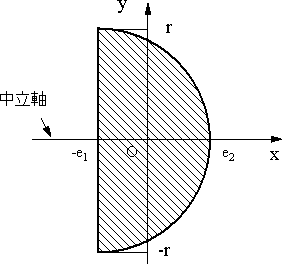
【解答例】
|
| 【問題13】 |
図の両端支持はりに、単位長さ当たりwの等分布荷重が作用するときに、せん断力、曲げモーメント、、せん断力図、曲げモーメント図を求め、次にたわみの式を求める。 |
|
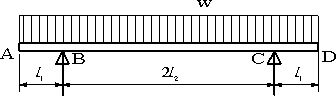
【解答例】
|
| 【問題14】 |
一辺の長さaの正方形断面のはりがy方向、鉛直方向に曲げを受けている。曲げモーメントが与えられたとき、最大応力を図のように斜線部をカットして、断面二次モーメントを変えて、応力を減少させることができるが、どの程度減少させることができるか求めよ。 |
|
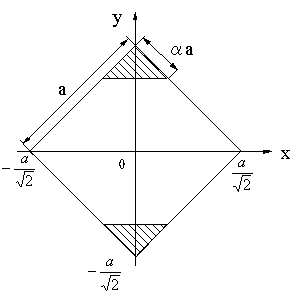 |
| |
【解答例】
|
| 【問題15】 |
400rpmで40PSを伝達可能な軸の直径を設計する。軸の材料の許容せん断応力を300MPaとする。また、軸のねじれ角を0.25°/m以内としたとき、軸の直径を求める。横弾性係数G=8.0×104 MPaとする。 |
|
【解答例】
|
| 【問題16】 |
長さL=3m 外径do=60mmの中空軸が回転角速度ω=60rad/s で、動力P=50kWを伝達している。
許容応力τ=100MPaで、ねじれ角θが0.05rad以下になるような安全な肉厚を求める。G=75GPaとする。 |
|
【解答例】
|
| 【問題17】 |
図の片持ちばりのたわみの式と最大たわみを求める。はりの断面二次モーメントI、ヤング係数Eとする。
●追加 せん断力図と曲げモーメント図を求める。 |
|
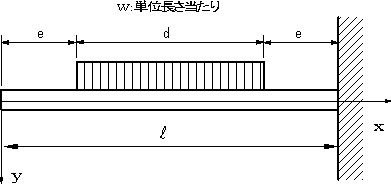 |
|
【解答例】
|
| 【問題18】 |
長さL=1.00m、幅w=50.0cm、厚さt=2.00mmの鋼製薄板の長手方向(x軸方向)と横方向(y軸方向)に同時にP=3.00×102kNの引張力が作用するとき
| (1). |
xy面内における垂直応力σx,σyとせん断応力τxyを求めよ。 |
| (2). |
x軸方向から反時計周りに45°回転した方向に法線を持つ面上に働く垂直応力σnとせん断応力τを求めよ。 |
| (3). |
)縦弾性定数E=2.00×10^2GPa、Poisson数を1/v=3.00とするとき、x軸方向の垂直ひずみεxとy軸方向の伸びλを求めよ。但し、Poisson数はPoisson比vの逆数である。 |
| (4). |
板厚の減少量dtを求めよ。 |
|
|
【解答例】
|
| 【問題19】 |
長さLの片持ちばりに自由端からaの範囲に単位長さ当たりwの等分布荷重が作用するとき、せん断力Vx, 曲げモーメントMxを求め、せん断力図と 曲げモーメント図を描く。 |
|
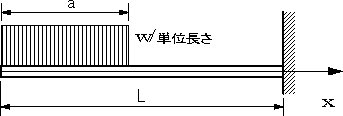
|
|
【解答例】
|
| 【問題20】 |
図1のような半円形断面の図心の位置C1,C2を求めた後、断面二次モーメントIxを求める。
|
|
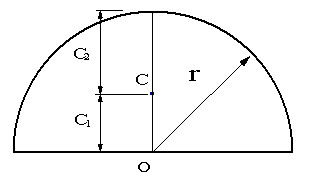
図1半径rの半円形断面 |
|
【解答例】
|
| 【問題21】 |
図のように段付き丸棒が両端を固定されている。この状態から |
|
(1)温度がΔT上昇したときに各部に生ずる応力を求める。 |
|
(2)温度がΔT降下したときに各部に生ずる応力を求める。 |
|
|
|
【解答例】
|
| 【問題22】 |
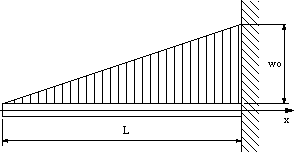
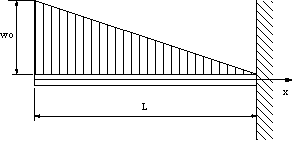
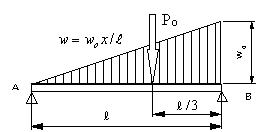
図の分布荷重の場合に、曲げモーメントを求める。
ただし、Poは作用している荷重ではなく、分布荷重の合力と作用点を示している。 |
|
|
|
【解答例】
|
【問題23】
|
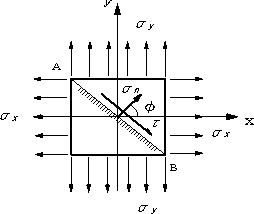
平面応力状態で、ある点の応力が、 σx=200[MPa]、σy=600[MPa]、τxy=40[MPa]であったとき、面の法線とx軸の角度がφ=60°の面上の、垂直応力とせん断応力を計算する。
|
|
【解答例】
|
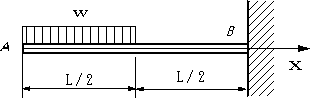
| 【問題24】 |
図の長さLの片持ちばりの自由端から半分の長さに単位長さ当たりwの等分布荷重が作用している場合に、せん断力Vx、曲げモーメントMx、たわみの式、自由端におけるたわみを求める。
|
|
|
|
【解答例】
|
| 【問題25】 |
長さ500mm、直径10mmの軟鋼丸棒に引張荷重が作用したとき、丸棒に生ずるひずみを0.1%以下になるようにする。縦弾性係数206GPa、材料の引張強さが400MPaである時
(1).許容応力σa, 許容荷重Pa を求める。
(2).安全係数nはいくつに設定していることになるか。 |
|
【解答例】
|
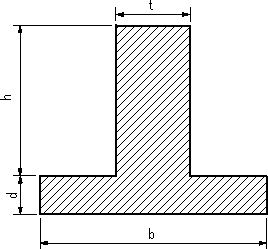
| 【問題26】 |
図面の図心を求め、断面二次モーメントIxを計算する。 |
|
|
|
【解答例】
|
| 【問題27】 |
図のように、微小要素に応力σx、σyが作用している。ヤング率をE=2.1×105MPa、ポアソン比をν=0.3としたとき、
|
| (1). |
σx=100MPa,σy=200MPaで平面応力のとき、x、y方向のひずみεx, εyを求める。 |
| (2). |
σx=100MPa,σy=-200MPaで平面ひずみのとき、x、y方向のひずみεx, εyを求める。 |
| (3). |
主応力σ1、σ2を(1)(2)の場合に求める。 |
| (4). |
最大せん断応力τmaxを(1)(2)の場合に求める。 |
|
 |
|
【解答例】
|
| 【問題28】 |
図のように、両端支持の梁(薄板、幅10mm、厚さ1mm)にモーメントPaを負荷し、長さLの部分が円周の1/4になるように円弧状に変形させる。このとき、梁に生ずる最大応力が許容応力σa=200MPaとする。縦弾性係数をE=200GPaとする。 |
| (1). |
この時のLを求めよ |
| (2). |
この時、梁に作用している曲げモーメントMと梁の曲率半径ρを求めよ。 |
|
 |
|
【解答例】
|
| 【問題29】 |
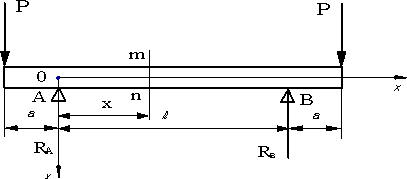
図の両端支持はりに、集中荷重PとモーメントMoが作用するとき、せん断力Vx,曲げモーメントMxとせん断力図,曲げモーメント図を求める。
ただし、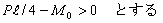 |
|
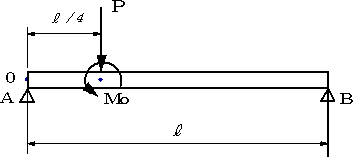 |
|
【解答例】
|
| 【問題30】 |
直径dの中実軸と外径do,内径diの中空軸の断面積が等しい。両者は同じ材料で剛性率Gとする。両軸にねじりモーメントTが作用するとき、中空軸のねじり剛性を中実軸の2倍にしたいとき、do/dの比を求めよ。 |
|
【解答例】
|
| 【問題31】 |
台形断面を持つはり(図)の図心の位置と断面二次モーメントを求めよ。 |
|
|
|
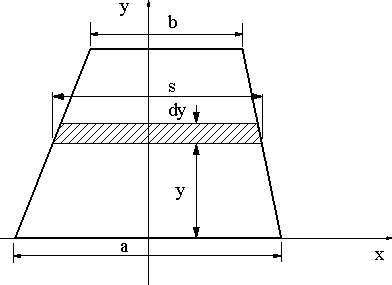 |
|
【解答例】
|
| 【問題32】 |
長さ2Lの両端支持はりで、左半分のはり(0≦x≦L)に、単位長さ当たり2qの等分布荷重が作用し、右半分のはり(L≦x≦2L)に単位長さ当たりqの等分布荷重が作用しているとき、せん断力、曲げモーメント、せん断力図、曲げモーメント図、最大曲げモーメントの生ずる位置と値を求める。
|
|
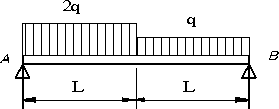
|
|
【解答例】
|
| 【問題33】 |
両端を固定された直径2r1,2r2の段付き丸棒にねじりモーメトTが作用するとき、それぞれの軸に生ずるせん断応力とねじり角を求める。
|
|
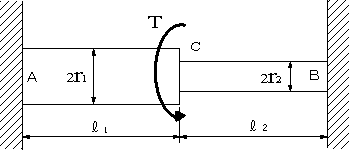
|
|
【解答例】
|
| 【問題34】 |
長さlの半径r1からr2に直線的に変化する軸にねじりモーメントT作用するとき、せん断応力とネジリ角を求める。
|
|
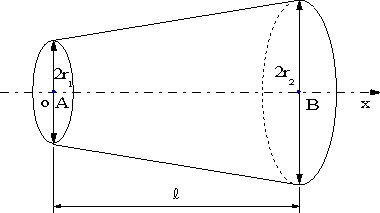
|
|
【解答例】
|
| 【問題35】 |
長さLの片持ちばりに単位長さ当たりwの等分布荷重が作用している。たわみの式と自由端のたわみを求める。次に、L=300mm,
幅b=300mm,厚さh=4mmのヤング係数E=3.30 GPaのアクリル板でwの合力が5kgfのとき、自由端のたわみを計算する。
|
|

|
|
【解答例】
|
| 【問題36】 |
直径dの丸軸が動力30kwを800 rpm で伝達している。軸の材料の許容せん断応力30MPaのとき、安全な軸の直径dを求める。
|
|
【解答例】
|
| 【問題37】 |
直径30mm、長さ80mmの丸軸がトルクを受け軸端で0.4°のねじれ角を生じた。このとき生ずるねじり応力τと軸に加わったトルクTを求める。軸の材料の横弾性係数は80GPaとする。
|
|
【解答例】
|
| 【問題38】 |
図のように、両端支持されている梁の中央に集中荷重Pが作用している。梁の断面は、内径di、外径doの中空円形断面の時、左半分の梁のたわみ曲線を求める。なお、縦弾性係数をEとする。
|
|
|
|
【解答例】
|
| 【問題39】 |
図のように、長さ1000mmの片持ち支梁において、梁全体に400N/mの等分布荷重と自由端に2kNの集中荷重、固定端か600mmの位置に3kNの集中荷重が作用している。材料の許容曲げ応力が157MPaのとき、安全な断面係数Zを計算する。
|
|
|
|
【解答例】
|
| 【問題40】 |
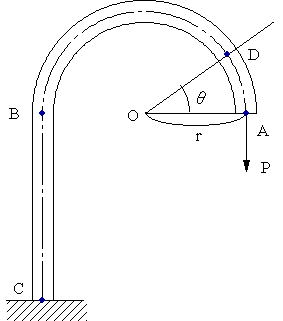
図のような梁に荷重Pが作用している。A,B点はOを中心とする半径rの円上にある。
(1).梁ABのD点を含むθ傾いた断面に生ずるせん断力、断面に垂直に作用する軸力、D点に作用する曲げモーメントを計算する。
(2).BCの梁の断面に作用するせん断力、断面に垂直に作用する軸力、D点に作用する曲げモーメントを計算する。
|
|
|
|
【解答例】
|
| 【問題41】 |
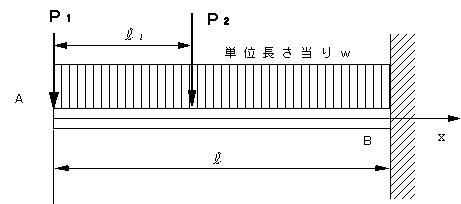
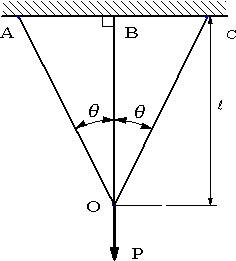
(1) .図1のように断面積A、ヤング率Eの棒材に、長さLのBOの下端Oに荷重Pが作用するときのO点の変位δを求める。
(2).BOの線膨張率αのとき、BOの温度がΔT上昇したときのO点の変位δを求める。荷重Pは作用していない。
|
|
|
|
【解答例】
|
| 【問題42】 |
重量W=100Nの剛体が、ワイヤーで吊るされてる。ワイヤの伸びを求める。線の長さはL=100m、直径d=
2 mmである。単位体積当たりの重量ρ=8000 kgf/m3、ヤング率E=210GPaとする。
|
|
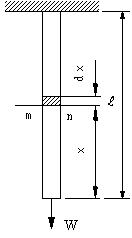
|
|
【解答例】 |
|
|
| 【問題43】 |
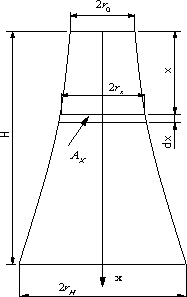
地上から高さH[m]のコンクリートのタワーを設計する。断面は円形とする。比重をρとする。最上部に重量Wのアンテナを載せる。
|
| (1). |
どの高さの断面上に生ずる圧縮応力σcが一定になるように円形断面の寸法を決める。 |
| (2). |
最上部の変位δを求める。 |
|
|
|
【解答例】
|
| 【問題44】 |
長さLのテ―パ付き丸棒を太いほうを上にしてつるす。直径は小さい方をd、大きい方をDとする。自重による伸びはいくらか。単位体積当たりの重量をw、弾性係数Eとする。直径は直線的に変化するとする。
|
|
【解答例】
|
| 【問題45】 |
直径dの軸が固定端からxの位置でトルクT=τo(1.2-x/L)を受けている。固定端からxの位置の断面内に生ずる最大せん断応力および先端のねじれ角φを求めよ。ただし、この丸軸の横弾性係数はGとする。
|
|
【解答例】
|
| 【問題46】 |
図のように、長さLの片持ち梁の下側に長さL1の断面形状・寸法が等しいはりを接着する。ただし、L>L1であり、断面は高さh、幅bの長方形断面である。生ずる最大応力を求める。
|
|
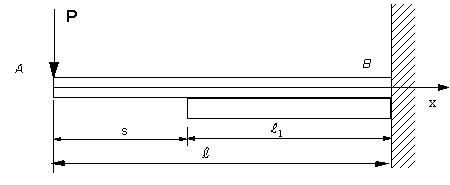
|
|
【解答例】
|
| 【問題47】 |
図のようにA点をとおる鉛直軸の周りを角速度ωで回転する長さLの軸の先端に重量Wの物体が負荷されている。軸の比重量γとして、遠心力によって生ずる応力を一定のσoになるように断面積Axを決める。
|
|
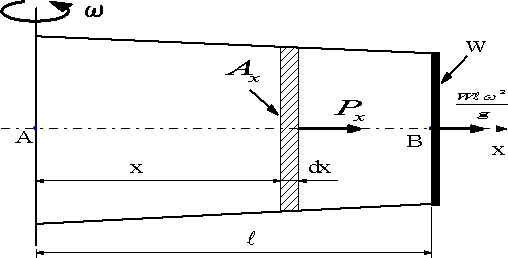
|
|
【解答例】
|
| 【問題48】 |
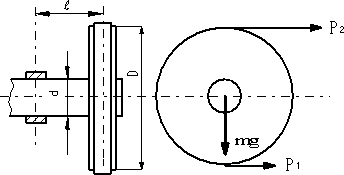
図(a)に示すように直径Dで質量mのベルト車に、引張側でP1=20kN,ゆるみ側でP2=5kNの張力がそれぞれ加わっている。 このベルト車の軸材に機械構造用炭素鋼S45Cを用いる場合、安全な軸径dを決める。なお、各部の寸法はベルト車の直径をD=500mm,質量M=100kg,ベルト車の幅方向の中央面から軸受(軸を止めている箇所)の中央面までの距離をL=100mmとして、軸受部での軸径dを求める。S45Cの引張強さσu=580MPa,せん断強さτu=460MPaとする。作用する力の考え方を図(b)に示す。 また、トルクT=(P1-P2)D/2とする。
|
|
 |
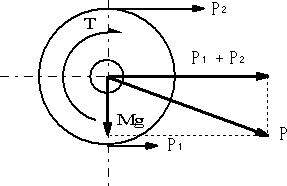 |
| 図(a) |
図(b) |
|
|
【解答例】
|
| 【問題49】 |
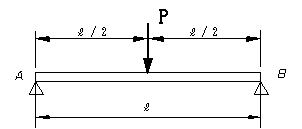
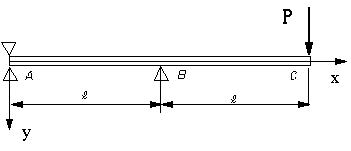
図のようなはりの場合にC点におけるたわみを求める。
|
|
|
|
【解答例】
|
| 【問題50】 |
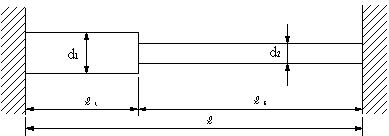
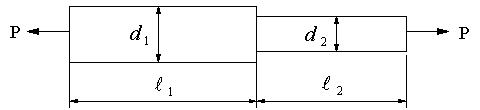
二つの異なる断面を有する段付き丸棒に引張荷重Pが作用している。この段付き丸棒の伸びδ
を計算する。この棒のポアゾン比v=0.3,ヤング率E=206GPaとする。d1=8mm,d2=6mm,L1=13mm,L2=14mm,F=2kN】
|
|
|
|
【解答例】
|
|

|