「はじめての材料力学」サポートページ >材料力学の典型的な問題 　PartⅢ

　　材料力学の典型的な問題 PartⅢ
　
　「はじめての材料力学」で提案している材料力学における「ミスの少ない計算」については、こちらをご覧下さい。
　片持ちばりの座標軸の取り方についてはこちらをご覧下さい。
　
　　　
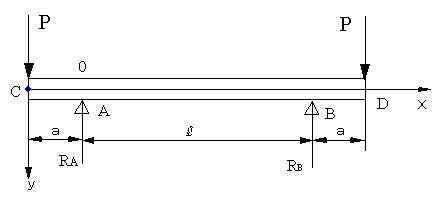
【問題101】 　図のような梁の場合に最大たわみとC点のたわみを求める。ただし、荷重P=147kN,a=183mm,L=800mm,
ヤング率E=2.05×105MPa,断面二次モーメントI=33.4cm4とする。
　

【解答例】
【問題102】 図1，図２の場合に、断面二次極モーメントを求める。
図1 図2
【解答例】
【問題103】 (1).図1の断面の断面二次モーメントIと断面係数Zを求める。b=15cm,h=20cm,c=9cm,d=15cm
(2).図2の単純支持はりの場合に、最大曲げモーメントが生ずる位置とその値、生ずる応力を求める。さらに、たわみ曲線と最大たわみを求める。ただし、 P=30kN, L=400cm,a=250cm.b=150cm,E=206GPa
図1 図2
【解答例】
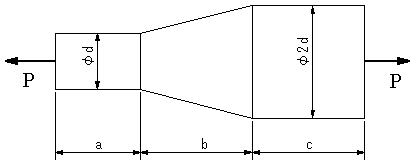
【問題104】 　図のように直径dの長さaの円柱の部分、直径dから2dに変化する長さbの部分、直径2dの長さcの円柱の部分からなる部材に引張荷重Pが作用する場合に、この部材の伸びを求める。ヤング係数をEとする。

【解答例】
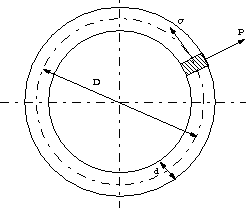
【問題105】 　平均直径D＝500mmの鋼製の円輪が回転数N=3000rpmで回転している。円輪の断面は直径d＝5mmの円形で、その密度をρ＝8000kg/m3、縦弾性係数をE=200GPaとするとき、
　
　（1）回転円輪の円周方向応力σを求めよ。
　（2）直径円輪の直径Dの変化ΔDを求めよ。

【解答例】
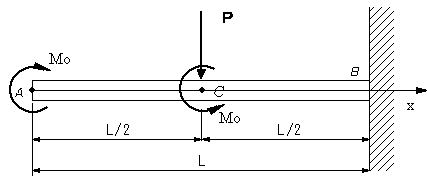
【問題106】 図の場合、たわみ角とたわみの式を求め、その後、B,C点のたわみ角とたわみを求める。


【解答例】
【問題107】 　直径100mmの軟鋼製の軸が100rpmの回転で、ねじりモーメントのほかに、1.5kN･mの曲げモーメントを受けるとき、伝達動力を求めよ。ただし、軸材の許容せん断応力は 、70MPaとし、最大せん断応力が先に許容せん断応力に達するものとする。
【解答例】
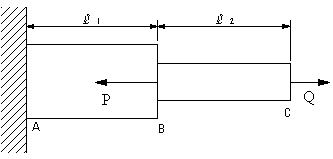
【問題108】 　　AB部の長さ l1=100cm、断面積A1=10cm2、BC部の長さl2=80cm、断面積A2=6cm2の段付き棒に関して以下の問いに答えよ。ただし、AB、BCは同じ材料で、縦弾性係数E=200GPaとする。 　図のように、A点が固定され、段付き部Bに荷重P=100kN、自由端Cに荷重Q=60kNを図の向きに受けるとき、B、C点の変位を求めよ。

　
【解答例】
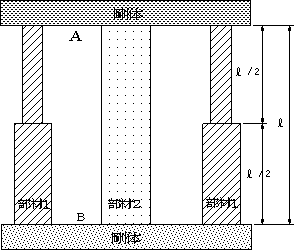
【問題109】 　 部材１，部材２はともに長さ２ｍ。部材２は断面積100mm2の軟鋼製の丸棒。部材１はアルミ製である。下半分の１mの部分の断面積は５００mm2上半分の1mの部分の断面積は200mm2。この構造の温度が100℃上昇したとき、円管と丸棒に生じる応力の最大値及びAB間の伸びを求めよ。
　アルミ（部材１）；線膨脹係数：αa=24×10-6/k,ヤング率：Ea=70GPa
　軟鋼（部材２）；線膨脹係数：αs=11×10-6/k,ヤング率：Es=200GPa

【解答例】
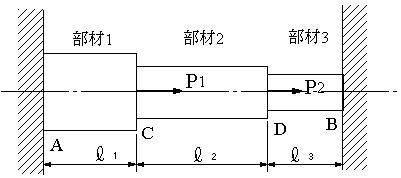
【問題110】 　両端が固定された状態で、接合点C、Dに荷重P1、P2が図に示した方向に作用するとき、部材１，２，３の応力及び、点C、Dの変位を求める。
　ただし、部材1，2，3の断面積、A1,A2,A3,長さをL1,L2,L3とする。部材1はアルミニウム、部材2は銅、部材3は軟鋼でそれぞれのヤング係数は、アルミニウムEA,銅Ec,軟鋼Esとする。

【解答例】
【問題111】
(1). 図1の場合の両端支持はりに等分布荷重wが作用するときに、せん断応力線図と曲げモーメント線図を求める。ただし、w=20N/cm, a=60cm
(2). 図2の場合の片持ち梁に等分布荷重w、集中荷重Wが作用するときに、せん断応力線図と曲げモーメント線図を求める。ただし、L=180cm, W=1000N,w=20N/cm
図1 図2
【解答例】
【問題112】
(1). 外径34mm肉厚3.2mmの鋼管に負荷できる最大ねじりモーメントを求めよ。ただし、許容せん断応力を24.5MPaとする。
(2). 長さおよび断面積の等しい、同一材料製の中実丸軸と中空丸軸において、負荷できるねじりモーメントおよびねじり剛性の比を求める。ただし中空軸の内径と外形の比は3：4とする。
【解答例】
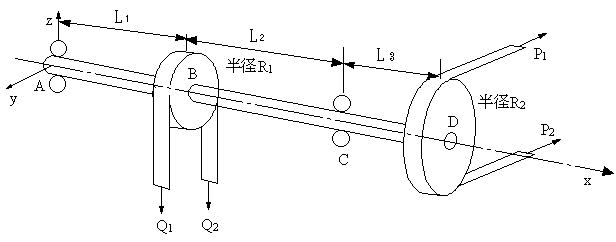
【問題113】 　軸受A,Cで支持されたL1=200mm,L2=300mm,L3=100mmの回転軸に、半径R1=100mmとR2=200mmの2つのプーリーが取り付けられている。プーリーの位置とベルトの張力を図のようにP1=200N,P2=340N、Q1=640N,Q2=360Nとしたとき、材料の許容引張応力110MPa、許容せん断応力50MPaとするとき、安全な軸径dを計算する。AとCは軸受けの位置である。

【解答例】
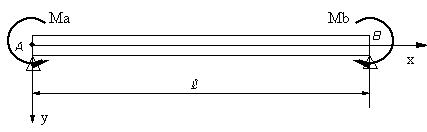
【問題114】 　両支点A,Bにそれぞれ曲げモーメントMa=10kN･m,Mb=20kN･mが加えられたとき、長さ4mの単純梁が ヤング係数E=20GPa, 断面の幅b=12cm,高さh=20cmであるとき、この梁の最大たわみが生ずる位置とたわみymaxを計算する。

【解答例】
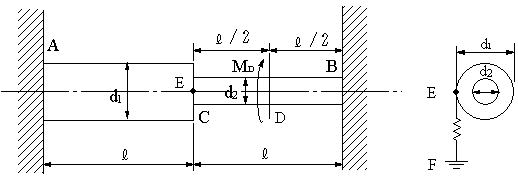
【問題115】 図のように半径2r、長さLの軸と半径r、長さLの軸が両端A、Bで固定されている。境界のC点において、図のようにE点でバネ定数定数kのバネに結合され、鉛直方向下で固定されている。CBの中間点DにトルクMDが作用している。バネによる力はE点において円周方向に作用すると考える。

【解答例】
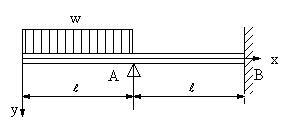
【問題116】 図の場合に、自由端のたわみを求める。

【解答例】
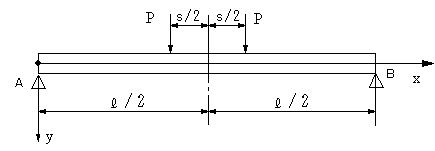
【問題117】 図の単純支持はりの場合に、0<x<L/2におけるたわみの式とx=L/2におけるたわみを求める。

　
【解答例】
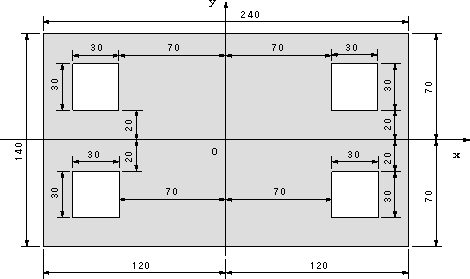
【問題118】 　横240mm、縦140mmの断面に、図のように、30mm×30mmの正方形の穴が４つ空いている。この断面のx軸に関する断面二次モーメントを計算する。

　
【解答例】
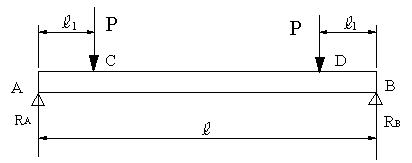
【問題119】 図の純粋曲げの場合、せん断力図、曲げモーメント図、たわみ曲線の式と、最大たわみを求める。

【解答例】
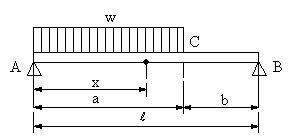
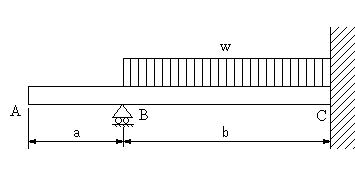
【問題120】 　図のように、AC間に単位長さ当たりwの等分布荷重が作用しいるとき、せん断力図、曲げモーメント図、最大曲げモーメントが生ずる位置とその値を求める。a>bとする。

【解答例】
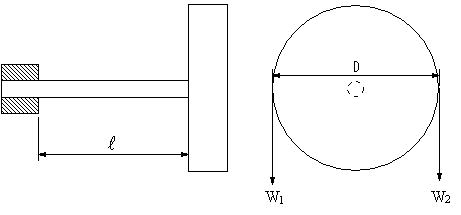
【問題121】 図のように、回転する軸に直径Dのプーリーが付いていて、これに、W1,W2の荷重が作用している。引張許容応力σa、せん断許容応力τaのとき、安全な軸の径dを求める。安全率αとする。ただし、W1=1960N,W2=490N,D=80cm,L=60cm,σa=206MPa,τa=147MPa,α=3 とする。

　
【解答例】
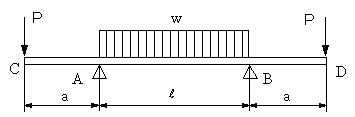
【問題122】 図の梁の場合に、せん断力図と曲げモーメント図を求める。

　
【解答例】
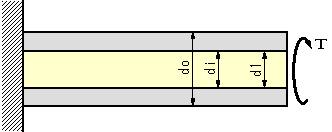
【問題123】 　直径ｄ1、横弾性係数はG1の丸棒に外径ｄo、内径ｄi、弾性係数はG2の円筒を接合した複合材料の軸がある。この複合材料の軸ABの一端Aを剛性壁に固定し、他端Bにトルク（ねじりモーメント）Tを加えるとき。円筒に作用するトルクT2および丸棒に作用するトルクT1を求めよ。ただし、 d1=diとする。

　
【解答例】
【問題124】 　外径60mm、内径30mmの中空軸がねじりを受ける。同じ材料で、この軸とせん断に対して同じ強さを有する中実軸の直径を求め、そして、中空軸の断面積は中実軸の断面積の何%になるか計算する。
【解答例】
【問題125】 直径60mmの中実丸軸とねじり強さが等しく、重さ70％である中空丸軸の外径と内径を求めよ。
【解答例】
　
【問題126】 　 断面形状が円形の長さ 3m の単純支持ばりに、重力による自重で曲げ応力が 24MPa になるようなはりの直径dを求める。ただし、丸鋼の単位面体積あたりの質量は 7.85×10-6kgf/㎜3 とする。
　また、この状態のはりの中央にさらに集中荷重を加え、はりに生じる最大曲げ応力を 135MPa 以下になるように、加えることができる集中荷重Pを求める。集中荷重だけによって、135－24＝101MPa の曲げ応力が生じているとして計算する。
【解答例】
【問題127】 　長さLoの線膨張係数の異なる材料を高温で接合し、温度がt℃低下した時、２つの材料に生ずる応力を計算する。ただし、線膨張係数α1,α2(α1<α2),断面積A1、A2、ヤング係数E1、E2とする。
　
【解答例】
【問題128】 (1).同一材料で同一断面積を有する中空丸棒の梁と、中実丸棒の梁の曲げモーメントに対する強さの比を求める。ただし、中空丸棒の内径は、外径の1/2とする。

(2). 外径40mm、内径20mmの中空軸は、等しい断面積を有する中実丸軸の何倍のトルクに耐えられるか求める。
【解答例】
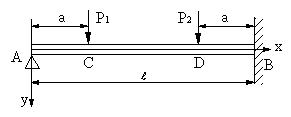
【問題129】 図の場合の梁のたわみ曲線を求める。

【解答例】
【問題130】 　外径40mm、内径20mmの中空軸は、等しい断面積を有する中実丸軸の何倍のトルクに耐えられるか求める。
【解答例】
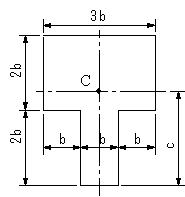
【問題131】 図のT型の図心と断面二次モーメントを求める。
　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　
【解答例】
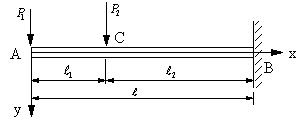
【問題132】 　図の片持ちばりの場合に、たわみの式を求める。

　
【解答例】
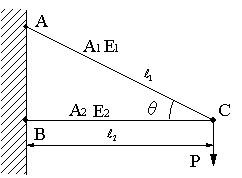
【問題133】 　図のように、A、B、Cでピン結合され、BCは剛体壁に対して直角、∠ACB=θである。P点に荷重Pが鉛直方向に作用している。棒AC、BCの長さ、断面積、弾性係数をそれぞれ、L1,L2,A1,A2,E1E2とするとき
(1).AC、BCに生ずる応力σ1、σ2を求める。
(2).AC、BCの伸びΔL1、ΔL2を求める。
(3).C点の水平方向、鉛直方向の変位量を求める。

【解答例】
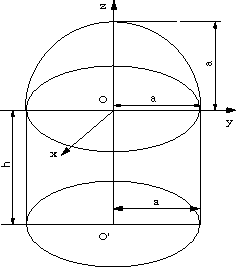
【問題134】 密度1.3g/cm3、半径a=18cm、高さh=24cmのエポキシ製円柱に、密度2.7g/cm3、半径a=18cmのアルミ製半球を図のように接着した。この連結体の重心(xG,yG,zG)を求めよ。ただしz軸を円柱の軸に一致させ、x,y面を接着面上にとるものとする。
【解答例】
　
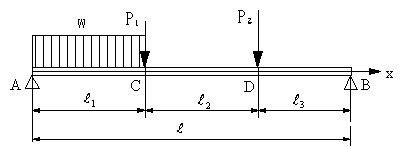
【問題135】 　図の両端支持はりの場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。最大曲げモーメントはAC間で生ずるものとする。

【解答例】
【問題136】 図の梁の場合のたわみの式と最大たわみを求める。
【解答例】
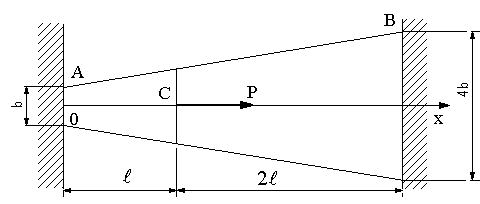
【問題137】 　 厚さt、 一方の幅b、他方の幅4b、長さ3Lの板が、図のように両端を剛体板で固定されている。C点に荷重Pが作用するとき、A点の反力Ra、B点の反力Rbを求める。弾性係数をEとする。


【解答例】
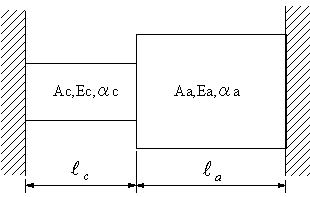
【問題138】 　 断面積Ac,弾性係数Ec,線膨張係数αcの銅製の棒と断面積Aa,弾性係数Ea,線膨張係数αaのアルミ製の棒が図のように接続され、両端が固定されている。温度がΔT上昇したとき、各部に生ずる応力を計算する。
　

【解答例】
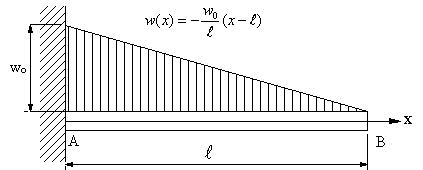
【問題139】 図のような分布荷重の場合に、せん断力、曲げモーメント、たわみ、最大たわみを求める。

【解答例】
【問題140】 図のはりのたわみ曲線の式とたわみの最大値を求める。

【解答例】
【問題141】 図(a),(b)の梁の場合のたわみ曲線を求める。

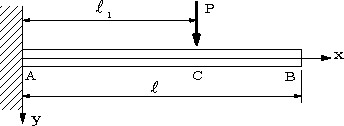(a)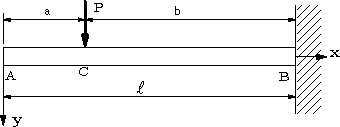

(b)
【解答例】
【問題142】 　底面の直径がd0の円錐状の弾性棒(長さL,ヤング率E,密度p)を、角速度ωで回転させる。棒の先端の変位を求めよ。

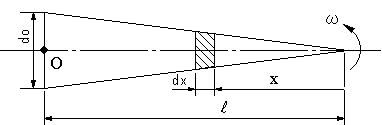【解答例】
【問題143】 図の梁の場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。ただし、L=1m,w=300N/m,P=500Nである。
　

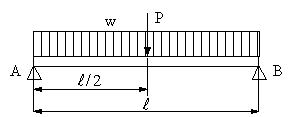【解答例】
【問題144】 　 図のように、ACとBCをC点でピン結合し、他端も固定壁にピン結合されている。C点に荷重Pが下向きに作用するとき、C点の変位を求める。　ただし、ACの長さ、ヤング係数、断面積をl1,E1,A1とし、BCの長さ、ヤング係数、断面積をl2,E2,A2とする。

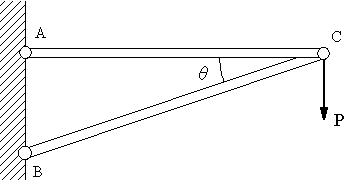【解答例】
　
【問題145】 　図の両端支持はりの場合に、せん断力Vx、曲げモーメントMxを求め、せん断力図、曲げモーメント図を描く。
　ただし、a=1m,P1=10kN,P2=7kNとする。

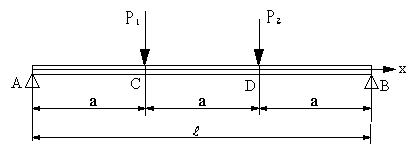【解答例】
【問題146】 　図のように、段付き丸棒と円筒からなる組合せ棒について考える。αは熱膨張係数である。段付き丸棒と円筒は同軸に配置して下端を剛体床に固定し、上端には平らな剛体板を接着することなく置く。ただし、段付き丸棒および円筒の自重と剛体板の重さは無視し、座屈は生じないものとする。
　（１）．段付き丸棒と円筒に生じる応力を求める。
　(２）．荷重Pが作用した状態で、温度がΔTだけ上昇したとき、段付き丸棒に生じる応力が０となるΔTの最小値を求める。

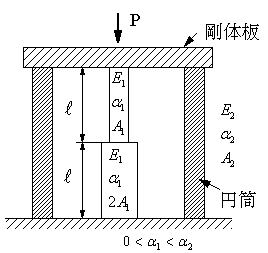【解答例】
【問題147】 　長さ3mの断面が円形の鋼の単純支持の場合に、自重によって生ずる曲げ応力を24MPaになるようにする。はりの直径を求める。ただし、はりの単位体積あたりの質量は7.85×10-6 kg/mm3とする。
【解答例】
【問題148】 図の場合に、せん断力と曲げモーメントを求める。

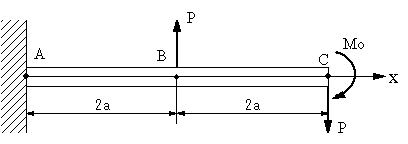【解答例】
【問題149】 　図の両端支持はりの場合に、せん断力と曲げモーメントを求める。

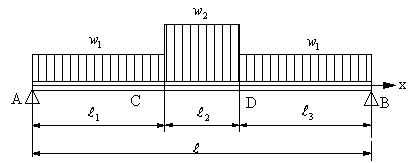【解答例】
【問題150】 図の場合のx軸、y軸に関する断面二次モーメントと断面係数を求める。

　
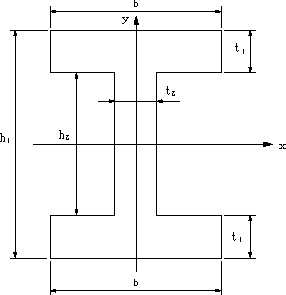【解答例】

「はじめての材料力学」サポートページ >材料力学の典型的な問題 　PartⅢ