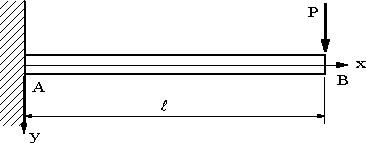
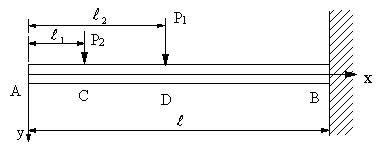
| 【問題250】 | 図の片持ちばりの場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図を求め、そして、たわみ曲線と自由端におけるたわみ角とたわみを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
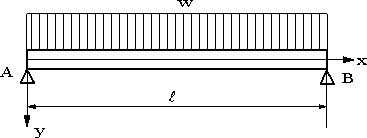
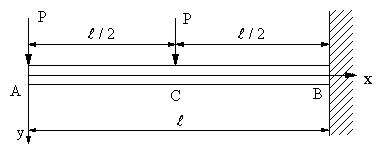
| 【問題251】 | 図の梁の場合に、たわみの式と自由端のたわみを求める。弾性係数と断面二次モーメントをE、Iとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
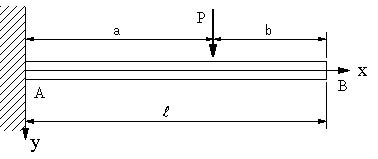
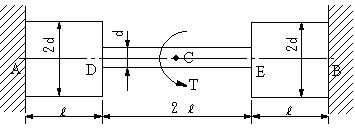
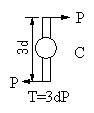
| 【問題252】 | 図のように、段付き丸棒が、両端A,Bにて剛体壁に固定されている。丸棒の中央Cに図のようにトルクT=3dPが作用している。A点に生ずるねじりモーメントとC点におけるねじれ角、せん断強さτaの時、安全な径を求める。 |
||||
  |
|||||
| 【解答例】 |
|||||
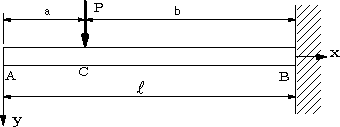
| 【問題253】 | 図の梁の場合に,たわみの式と最大たわみを計算する。 |
||||
|
|||||
| 【解答例】 |
|||||
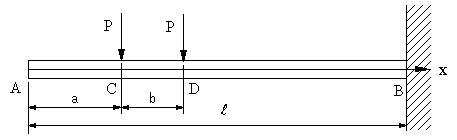
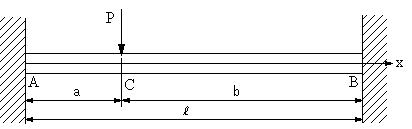
| 【問題254】 | 図の梁の場合に、最大曲げモーメント、せん断力と曲げモーメント、せん断力図と曲げモーメント図、たわみ曲線を求める。但し、a<bとする | ||||
 |
|||||
| 【解答例】 |
|||||
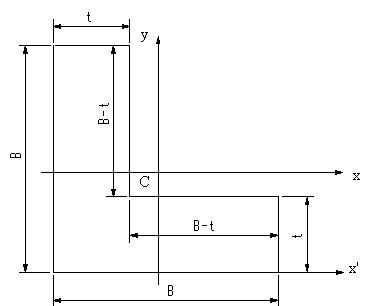
| 【問題255】 | 図のL型断面の図心の位置(上編、下辺からの距離)と断面二次モーメントと断面係数を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 【問題256】 | 図(a),(b)の梁の場合に、たわみ曲線の式と、自由端のたわみを求める。 |
||||
|
|||||
| 【解答例】 |
|||||
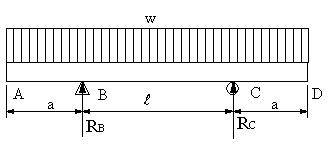
| 【問題257】 | 図の梁の場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図、最大曲げモーメントが生ずる位置とその値を求める。単位長さ当たりwの等分布荷重とする。 |
||||
 |
|||||
| 【解答例】 |
|||||
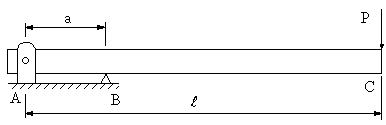
| 【問題258】 | 図のような梁の場合に、最大曲げモーメントとの生ずる位置とその値、せん断力図、曲げモーメント図を求め、自由端のたわみを計算する。但し、梁の長さL=2m,a=50cm,P=500N,梁の断面は直径d=5cmの円形、梁の材質は木製でヤング率E=10GPaとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
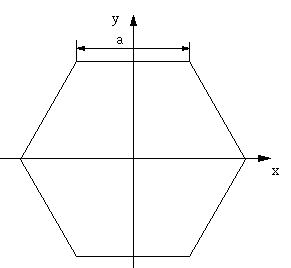
| 【問題259】 | 図の一辺aの長さの正六角形の断面の図心の位置、断面二次モーメント、断面係数を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
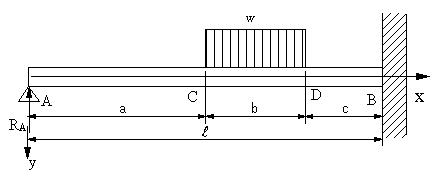
| 【問題260】 | 図の不静定梁の場合にたわみの式を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
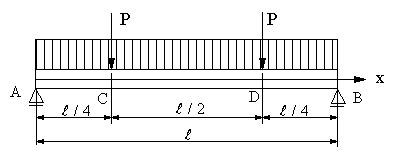
| 【問題261】 | 図の梁の場合にせん断力、曲げモーメント、せん断力図、曲げモーメント図、最大曲げモーメントの値を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
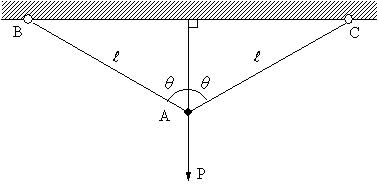
| 【問題262】 | 図のように回転自由に結合された長さl,断面積A、ヤング係数Eの2本の軟鋼丸棒がある。A点に荷重PをBCに直角な方向に加える時、棒に生ずる応力とA点の鉛直方向の変位を求める。変位は小さいものとして計算する。 |
||||
 |
|||||
| 【解答例】 |
|||||
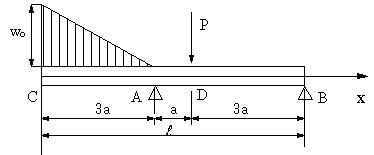
| 【問題263】 | 図の梁の場合に、支点の反力とせん断力、曲げモーメントを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
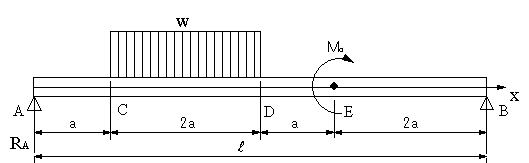
| 【問題264】 | 図の梁の場合に、支点の反力とせん断力、曲げモーメントを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
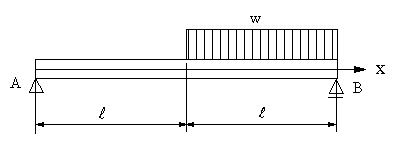
| 【問題265】 | 図の梁の場合に、せん断力、曲げモーメント、最大曲げモーメントの値、せん断力図、曲げモーメント図を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
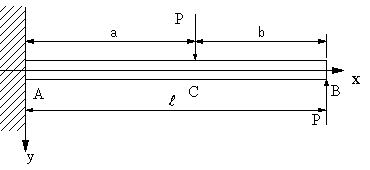
| 【問題266】 | 図の梁の場合に、たわみの式と、x=L,x=aにおけるたわみの値と最大たわみを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
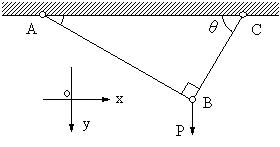
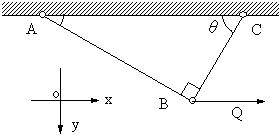
| 【問題267】 | 図1,図2の場合に、AB,BCの長さ、断面積、ヤング率をL1,L2.A1,A2, E1,E2とする。∠ABC=π/2,∠BCA=θとするときに、図1では荷重Pが垂直下方に、図2では水平方向に荷重Qが作用するときに、B点のx方向の変位とy方向の変位を求める。 |
||||
|
|||||
| 【解答例】 |
|||||
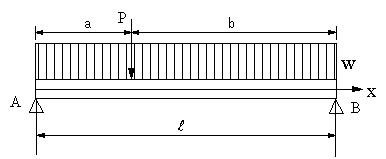
| 【問題268】 | 図の梁の場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図、最大曲げモーメントの値を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
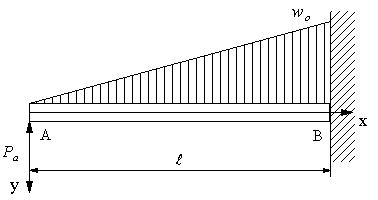
| 【問題269】 | 図の片持ち梁の場合に、A点に上向きの荷重を加えてA点のたわみを0にする時、荷重の大きさを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
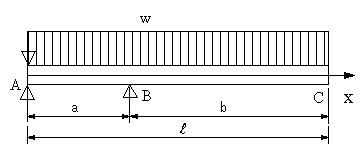
| 【問題270】 | 図の梁の場合に、弾性係数E、断面二次モーメントIとして、C点におけるたわみを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
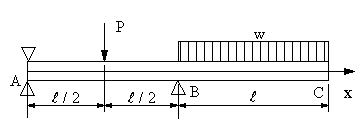
| 【問題271】 | 図の梁の場合に、各支点の反力、せん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。 P=wLとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
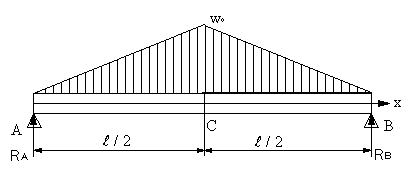
| 【問題272】 | 図の梁の場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
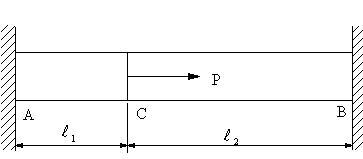
| 【問題273】 | 断面積A、ヤング率Eの棒、AC,BCが図のように剛体壁に両端を固定されている。長さは、ACはL1、BCはL2
である。Cに荷重Pが作用したとき、AC,CBに作用する荷重、AC,CBに生ずる応力、C点の移動量を計算する。 |
||||
 |
|||||
| 【解答例】 |
|||||
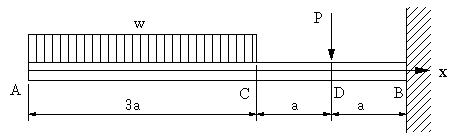
| 【問題274】 | 図の片持ち梁の場合、w=5kN/m,P=20kN,a=1mの時、固定壁のB点に生ずる反力RB、反モーメントMB、 せん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
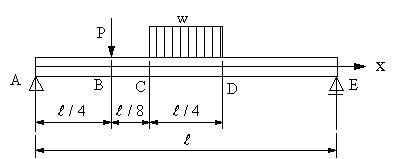
| 【問題275】 | 図の梁の場合に、支点の反力、せん断力、曲げモーメントを求める。また、 w=P/Lである場合に,x = L/2における曲げモーメントを求め.る。 |
||||
 |
|||||
| 【解答例】 |
|||||
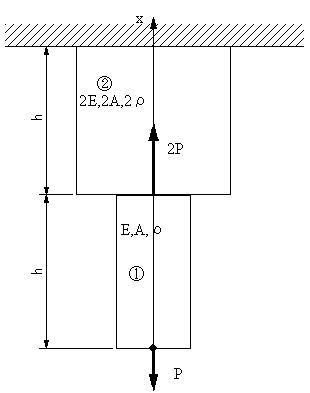
| 【問題276】 | 上部が固定されている①,②の棒にP,2Pの荷重が作用している。自重を考慮し、生ずる応力と伸びをxの関数として求める。また、全体の伸びを求める。ただし、密度ρ、ヤング率E、面積Aとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 【問題277】 | 図の梁の場合に、固定端Bに生ずる反力とモーメントを求め、せん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。次に、梁の断面二次モーメントを求める。最大曲げモーメントを求め、梁に生ずる最大引張応力を計算する。 |
||||
|
|||||
| 【解答例】 |
|||||
| 【問題278】 | 密度ρの棒の上端を天井に固定して吊り下げて、下端に引張り荷重Pが作用し、下端での断面積をAoとした場合、棒のどこの断面でも一定の応力σが生ずるようする。断面は円形で、最下端では断面積Aoとして、断面積を表す式を求める。 |
||||
| 【解答例】 |
|||||
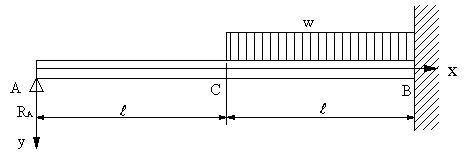
| 【問題279】 | 図の不静定ばりの場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図、最大曲げモーメント、たわみの式を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
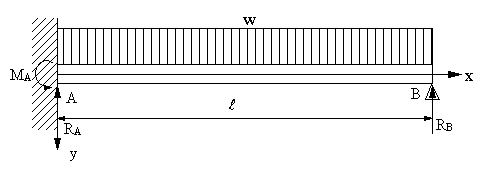
| 【問題280】 | 図の梁の場合に、Aにおける反力、反モーメント、Bにおける反力を求める。ヤング率E,断面二次モーメントIとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
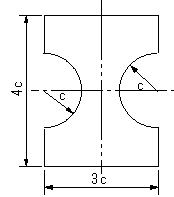
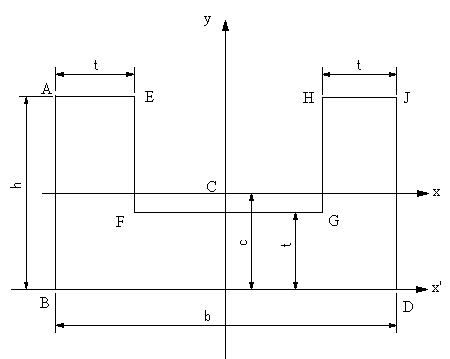
| 【問題281】 | 最終的に平行軸の定理により、凹型図形の断面二次モーメントを求めるために、以下の順で値を計算する。 断面図形の面積、x’軸周りの断面一次モーメント、x'軸から図心までの距離、図形ABDJ,EFGHの各々の図心に関する断面二次モーメント、図形ABDJ,EFGHの図心Cに関する断面二次モーメント、凹型図形の断面二次モーメントを求め、そして、図心Cより下側と上側の断面係数を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
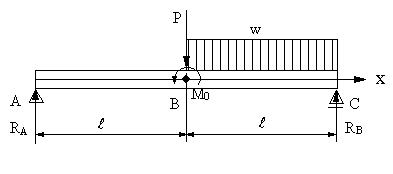
| 【問題282】 | 図の梁の場合に、支点の反力、せん断力、曲げモーメント、せん断力図、曲げモーメント図、最大曲げモーメントを求める。ただし、w=P/L,Mo=PLとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
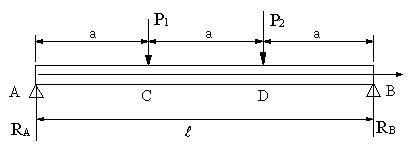
| 【問題283】 | 下記の梁の時、たわみの式を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
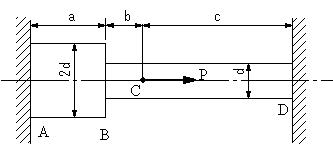
| 【問題284】 | 図のように直径2dとdの軸がA,D点で剛体壁に固定されている。C点に荷重Pが作用するとき、A点とD点の反力とC点の変位量を求める。AB,BD材のヤング率E1,E2とする。 |
||||
 |
|||||
| 【解答例】 |
|||||
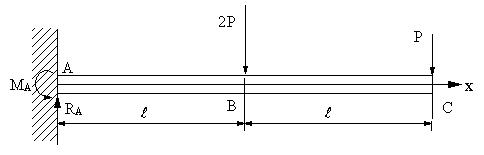
| 【問題285】 | 図の梁の場合に、固定端の反力とモーメント、せん断力、曲げモーメント、せん断力図、曲げモーメント図、最大曲げモーメントを求める。梁の断面が外径d,肉厚tの中空円形の場合に、断面二次モーメントと断面係数,最大曲げモーメントが生ずる位置と値、その位置の曲げ応力を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 【問題286】 | 図に示すような段付きの円筒軸を考える。全域にわたり、内径Dである。円筒軸の片端は剛壁Aに固定されている。応力集中を無視する。部材の横弾性係数をGとする。図のように細い剛部材を連結し、それぞれ図の方向に荷重P及びFを作用させる。部材の長さ2L,Lは、軸の中心軸から測った長さを示す。 この部材の許容せん断応力をτaとする。F=P/2とするとき、Pによる許容ねじりモーメント値Paを求める。このとき、F=P/2として、軸の先端に生じるねじれ角度の大きさφを求める。 |
||||
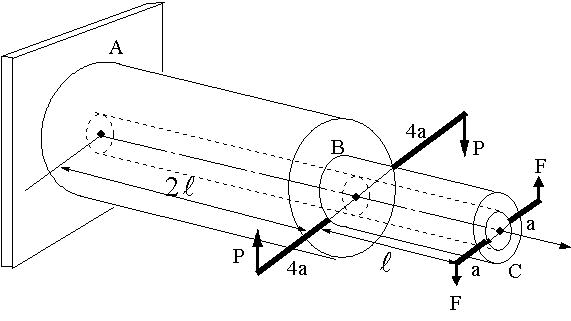 *4a,aは軸心からP,Fの力が働く作用点までの距離である。 |
|||||
| 【解答例】 |
|||||
| 【問題287】 | 下図において、棒①、棒②はA,Cで剛体壁に固定されている。①のみがΔTだけ加熱された場合における各棒の応力σ1とσ2を求める。断面積はそれぞれS1,S2で,縦弾性係数がそれぞれE1,E2とする。線膨張係数はαである。 |
||||
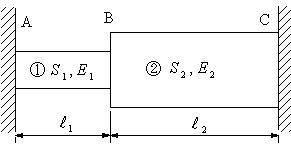 |
|||||
| 【解答例】 |
|||||
| 【問題288】 | 図のように、回転数N=200rpmでP=200kWを伝達できるモーターにAで接続された軸に、ギアーB,Dでそれぞれ、P1=90kw, P2=110kWが消費される。軸材の許容せん断応力σa=50MPaとして、D端でねじり角がφ=1.5°以下になる最小の軸径dを求める。軸材の横弾性係数をG=80GPaとする。L1=1.8m,L2=1.2mとする。 |
||||
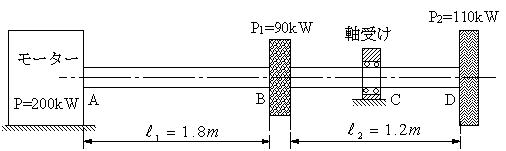 |
|||||
| 【解答例】 |
|||||
| 【問題289】 | 図の場合、AB、BCに生ずる応力と、B点の垂直変位と水平変位を求める。 |
||||
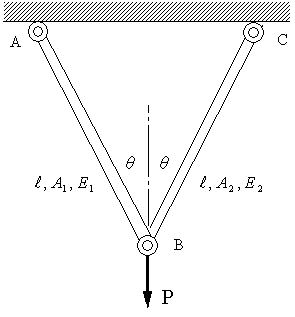 |
|||||
| 【解答例】 |
|||||
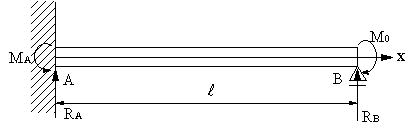
| 【問題290】 | 図のようにB点にモーメントMoが作用する不静定な片持ち梁の場合に、各支点の反力、モーメント、せん断力、曲げモーメントせん断力図、曲げモーメント図を求める。
L=6m,Mo=300kN・m,ヤング率E,断面二次モーメントIとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
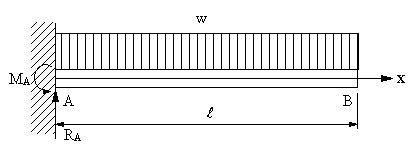
| 【問題291】 | 矩形断面の幅b、高さhの片持ち梁に単位長さ当たりwの等分布荷重が作用するとき、固定点の反力、モーメントを求め、せん断力、曲げモーメント、せん断力図、曲げモーメント図、Aからxの位置の断面に生ずる引張応力とその最大値を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
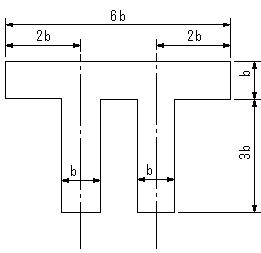
| 【問題292】 | 図において、下辺からの図心の位置と断面二次モーメントを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 【問題293】 | 図のような両端支持梁の場合に、せん断力、曲げモーメントとせん断力図、曲げモーメント図を求める。P=100N |
||||
 |
|||||
| 【解答例】 |
|||||
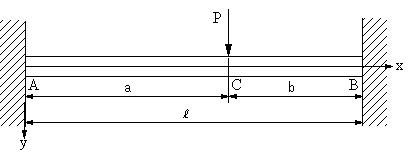
| 【問題294】 | 図の両端固定梁の場合に、たわみの式とたわみが最大となる位置と最大たわみを求める。但し、a>b、弾性係数E、断面二次モーメントIとする。 | ||||
 |
|||||
| 【解答例】 |
|||||
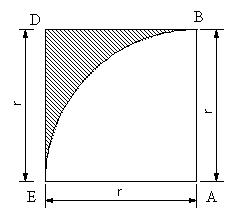
| 【問題295】 | 図においてABDEは一辺rの正方形。ABEはAを中心とする半径rの円の1/4である。円の一部はB,E点において正方形に接している。斜線の部分の図心と断面二次モーメントを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
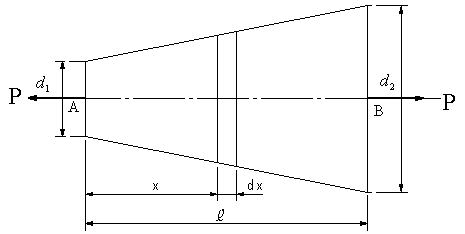
| 【問題296】 | 図のように直径が異なる円柱の両端に荷重Pが作用するとき、Aからxの位置に生ずる応力と全体の伸びを求める。ヤング率Eとする。 | ||||
 |
|||||
| 【解答例】 |
|||||
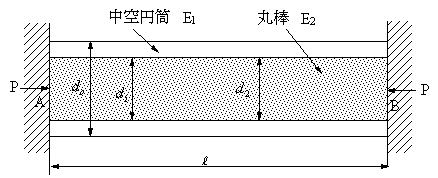
| 【問題297】 | 図のように外径do=100ミリ、内径di=60ミリの中空円筒1と、直径d2=60ミリの丸棒2を組み合わせた(中空円筒1の中に丸棒2を入れた状態)長さL=500ミリの部材がある。この両端に変形を無視できる剛体を介して、P=200kNの圧縮荷重が作用している。中空円筒1の縦弾性係数をE1=200GPa、丸棒2の縦弾性係数をE2=100GPaとして、それぞれの材料に発生する応力と部材全体の圧縮量を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
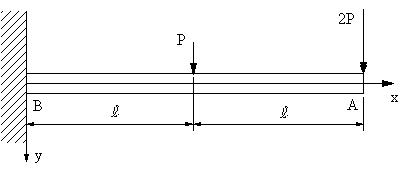
| 【問題298】 | 図の梁の場合に、たわみ角とたわみの式を求め、A点におけるたわみを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
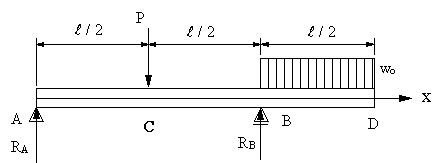
| 【問題299】 | 図の梁の場合にせん断力図、曲げモーメント図を求める。ただし、P>woL/4とする。 | ||||
 |
|||||
| 【解答例】 |
|||||
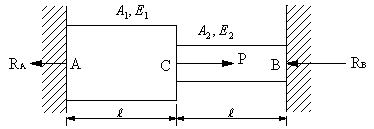
| 【問題300】 | 図のように、断面積A1,A2、弾性係数E1,E2の棒が剛体壁に固定されている。固定点A、Bに生ずる反力RA,RBを求める。 |
||||
 |
|||||
| 【解答例】 |