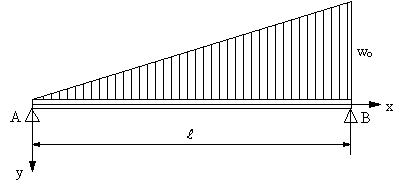
| 【問題200】 | 図の両端支持はりの場合に、たわみの式を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
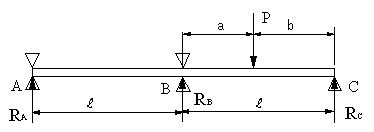
| 【問題201】 | 図の不静定梁の場合に、各支点における反力とたわみ角、たわみの式を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
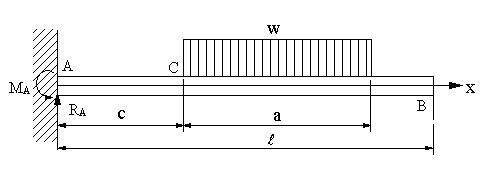
| 【問題202】 | 図の片持ちばりの場合にせん断力と曲げモーメント、せん断力図と曲げモーメント図を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
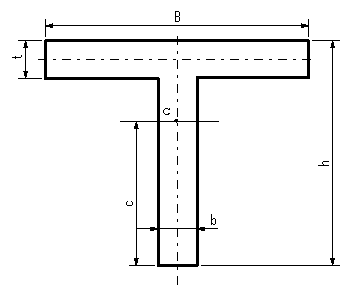
| 【問題203】 | 図のT型断面の図心と、断面二次モーメント、断面係数を計算する。 |
||||
 |
|||||
| 【解答例】 |
|||||
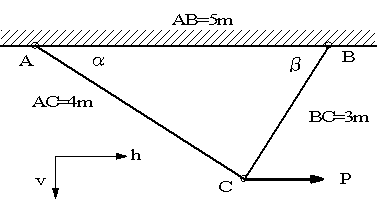
| 【問題204】 | 図に示すように、長さAC=4mの鋼棒と長さBC=3mの鋼棒を端Cでピン結合し、他端A,BをAB=5mの間隔に保って剛性天井にピンで結合する。結合点Cに水平荷重P=80kNが作用するとき、点Cに生じる水平および鉛直変位δh、δvを求めよ。ただし両棒の横断面積をA=10cm2、縦弾性係数Eを2.1x105MPaとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
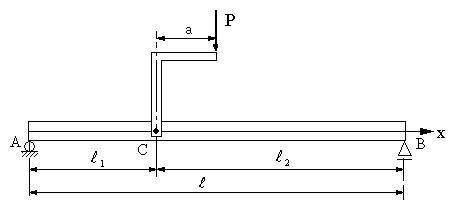
| 【問題205】 | 図の両端支持はりの場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。ただし、a<L2 |
||||
 |
|||||
| 【解答例】 |
|||||
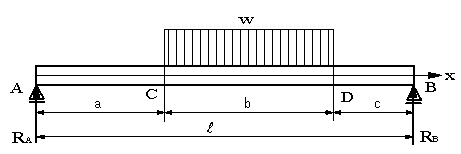
| 【問題206】 | 図の両端支持はりの場合、せん断力、曲げモーメント、せん断力図、曲げモーメント図、曲げモーメントの最大値と生ずる位置を求める。 | ||||
 |
|||||
| 【解答例】 |
|||||
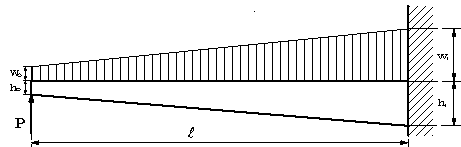
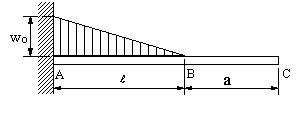
| 【問題207】 | 図のような、自由端で高さho、固定端で高さh1の幅bのはりに、自由端でwo,固定端でw1の分布荷重とPの集中荷重が自由端で作用するとき、自由端からxの位置に生ずるせん断力、曲げモーメント、生ずる応力を計算する。次に、自由端からxの位置に生ずるたわみを求める。たわみを求めるとき、計算を簡単にするために、ho=0として計算する。 |
||||
 |
|||||
| 【解答例】 |
|||||
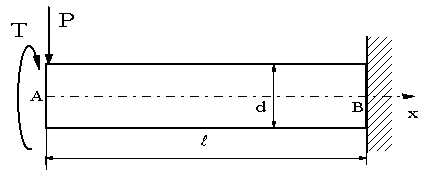
| 【問題208】 | 円形断面(直径d = 40mm,長さl = 200mm )の片持ちはりに、自由端に曲げ荷重Pb =200kgfとトルクT = 50000kgf・mmが同時に作用する場合、固定端に生ずる主応力σ1,σ2と最大せん断応力を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
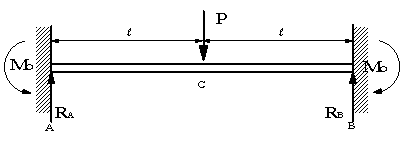
| 【問題209】 | 図の両端固定梁の場合にたわみ角とたわみ、最大たわみを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
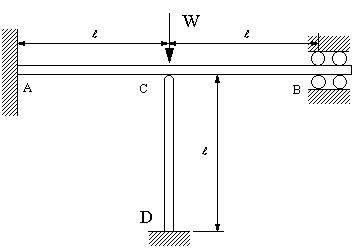
| 【問題210】 | 図の梁の場合にC点のたわみを求める。AB,CD材は弾性係数E,断面二次モーメントI,,CD材の断面積をAとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
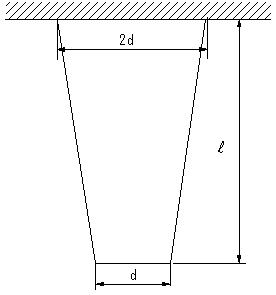
| 【問題211】 | 図のように、直径が 2d [m]、自由端の直径がd [m]の円形断面の棒が上端部を固定されている。全体の長さはL [m]である。この棒材の縦弾性係数をE [pa]、密度をρ[kg/m3] とするとき、自重による全体の伸びδ[m] を求める。ただし、重力加速度をg[m/s2] とする。 |
||||
 |
|||||
| 【解答例】 |
|||||
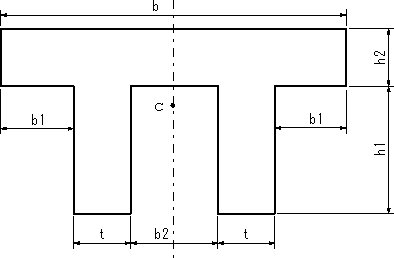
| 【問題212】 | 図の断面形状の場合に、断面二次モーメントを計算する。 |
||||
 |
|||||
| 【解答例】 |
|||||
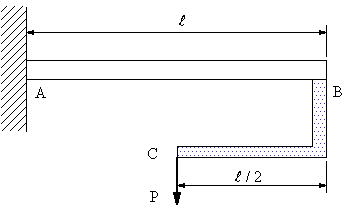
| 【問題213】 | 図の梁の場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。BC材は剛体とする。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 【問題214】 | 図の梁の場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 【問題215】 | 図の梁の場合に、たわみの式と自由端におけるたわみを求める。 |
||||
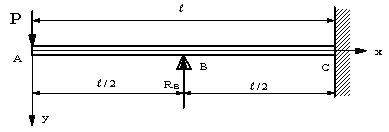 (aI |
|||||
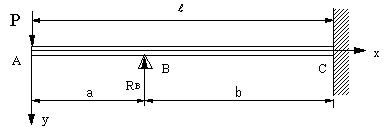 (b) |
|||||
| 【解答例】 |
|||||
| 【問題216】 | 図の不静定梁の場合に、反力RA,モーメントMA,たわみ曲線を求める。 |
||||
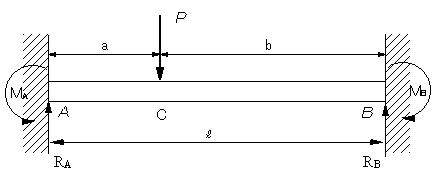 |
|||||
| 【解答例】 |
|||||
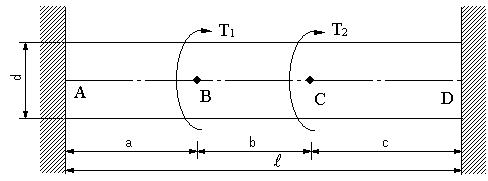
| 【問題217】 | 図のように両端が固定されている軸に、ねじりモーメントT1,T2が作用するとき、軸AB,BC,CDに作用するねじりモーメント、各軸のねじれ角、各軸に生ずるせん断応力を求める。剛性率G,断面二次極モーメントJ,極断面係数Zp
,T1>T2とする。 |
||||
 |
|||||
| 【解答例】 |
|||||
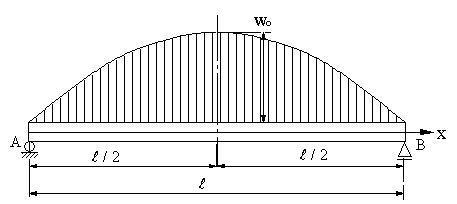
| 【問題218】 | 分布荷重が図のように二次関数(放物線)的に変化する場合に、曲げモーメントとたわみ曲線、最大たわみを求める。分布荷重の最大値は図のようにwoとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
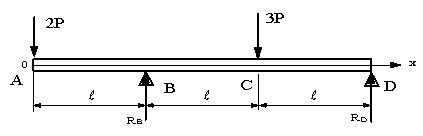
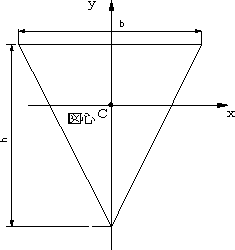
| 【問題219】 | 図の梁の場合にせん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。次に、最大曲げモーメントの値と生ずる位置を求め、その位置に生ずる最大応力(断面係数Z1)、最小応力(断面係数Z2)を計算する。次に、梁の断面形状が図の場合の断面二次モーメント、断面係数を求める。 |
||||
  |
|||||
| 【解答例】 |
|||||
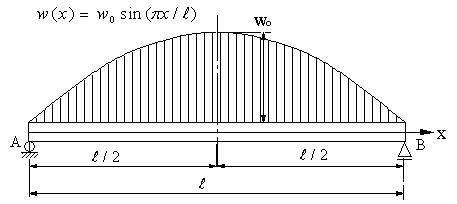
| 【問題220】 | 分布荷重が図のように、三角関数(sin関数)として変化する場合に、曲げモーメントとたわみ曲線、最大たわみを求める。分布荷重の最大値は図のようにwoとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
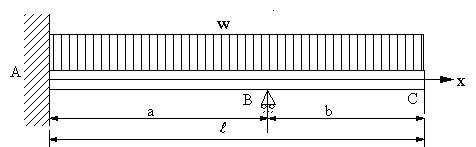
| 【問題221】 | 図に示す梁の場合に、支点Bの反力、たわみ曲線、C点のたわみを求める。惰性係数E,断面二次モーメントIとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
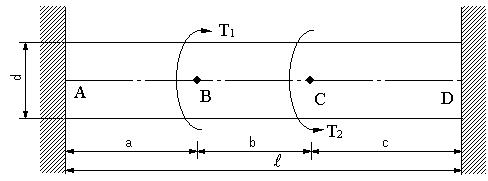
| 【問題222】 | 図のように両端が固定されている軸に、ねじりモーメントT1,T2が作用するとき、軸AB,BC,CDに作用するねじりモーメント、各軸のねじれ角、各軸に生ずるせん断応力を求める。剛性率G,断面二次極モーメントJ,極断面係数Zp ,T1>T2とする。 |
||||
 |
|||||
| 【解答例】 |
|||||
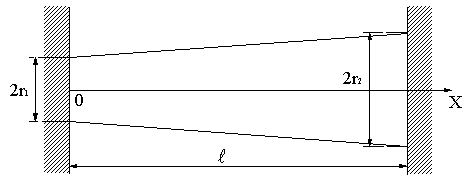
| 【問題223】 | 図のように両端を剛体壁に挟まれた円形断面でその半径が壁の間で線形的に変化する長さLの棒の場合、ΔTの温度上昇したとき、この棒に発生する最大圧縮応力の値と位置を求める。 縦弾性係数はE,線膨張係数はα、半径はr1,r2とする。ただし、r1<r2 |
||||
 |
|||||
| 【解答例】 |
|||||
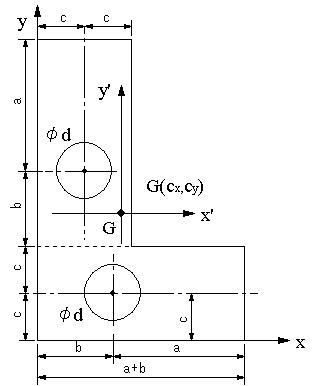
| 【問題224】 | 図aのようにL型形状の板に直径dの穴が2個ある場合に、図心Gのx,y座標を求め、断面二次モーメントIx,Iyを計算する。 |
||||
 |
|||||
| 【解答例】 |
|||||
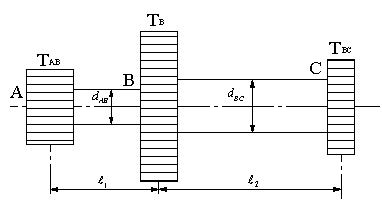
| 【問題225】 | 動力源からPB=15kWの動力が歯車Bに伝えられ、軸の回転数はN=1500r.p.m.である。歯車BからL1=0.2m離れた歯車AにPAB=9kWの動力が、L2=0.4m離れた歯車CにPBC=6kWの動力を伝える。中実軸の横弾性率G=82GPa、許容せん断応力τa=30MPaである。 両軸のたわみ角φ=0.1°のとき、両軸の大きさを求め、この時、両軸に生ずる生ずるせん断応力が許容せん断応力以下であることを示せ。 |
||||
 |
|||||
| 【解答例】 |
|||||
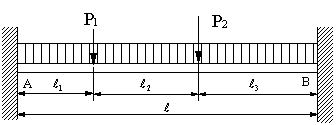
| 【問題226】 | 図の梁の場合にたわみの式を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
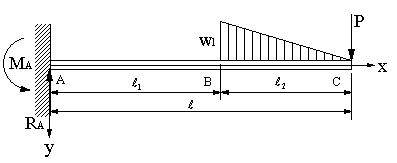
| 【問題227】 | 図の梁の場合に、RA,MA.たわみの式を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
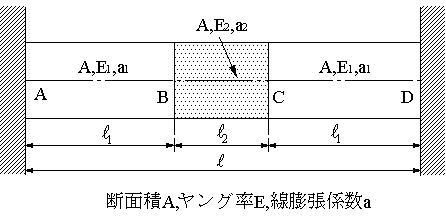
| 【問題228】 | 図のように両端が壁に拘束された断面積Aの複合棒がある。この状態から温度ΔTだけ上昇した場合、生ずる応力と棒ABおよび、BCの伸びλab、λbcをそれぞれ求める。 ただし、棒AB、CDの線膨張係数をa1、ヤング率をE1、棒BCの線膨張係数をa2、ヤング率をE2とする。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 【問題229】 | 図の梁の場合にせん断力、曲げモーメント、C点のたわみを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
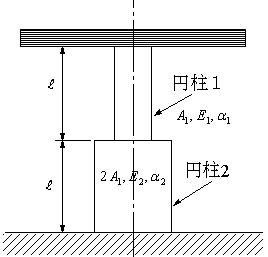
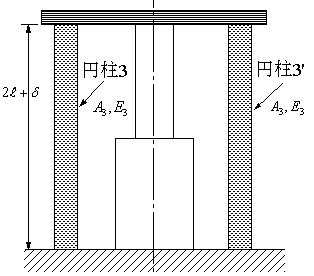
| 【問題230】 | 図1において、上部の剛体板は段付き棒に固定されている。 (1)図1の段付き棒の温度⊿T上昇させ、上部の剛体板の位置をδだけ上昇させる。このとき、δを⊿Tであらわす。 (2) (1)の状態で2L+δの円柱2本を剛体板と床の間に挿入する。この状態から段付き棒の温度をT+⊿TからTに下げた時に円柱1,2,3に生じる応力をそれぞれ求める。 |
||||
|
|||||
| 【解答例】 |
|||||
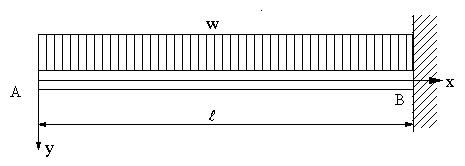
| 【問題231】 | 図の等分布荷重wが作用する片持ち梁の場合に、梁の断面形状は辺の長さaの正方形として、 (1).せん断力、曲げモーメントの式を求め、 (2).曲げモーメントの最大値を求め、生ずる最大応力を求める。 (3).たわみの式を求め、最大たわみδmaxを求める。 ヤング係数E、断面二次モーメントIと置いても良い。 (4).更に、自由端に集中荷重Pを作用させ、たわみをδ(δ<δmax)のとき、Pの大きさを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 【問題232】 | 図の梁の場合に、支点の反力、断面二次モーメント、各部に生ずる応力の大きさを求める。但し、断面係数をZとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
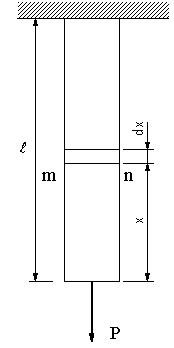
| 【問題233】 | 長さL, 断面積A=1.20cm2の棒の上端を固定し、下端にP=60.0kgfの荷重を作用させ、自重による応力を考慮し、棒に生ずる最大応力σmax=147 MPa となるときの棒の長さLと伸びδを求める。ただし、棒の材料の比重量γ=7.80×10-3 kgf/cm3,縦弾性係数E=206GPa とする。 |
||||
 |
|||||
| 【解答例】 |
|||||
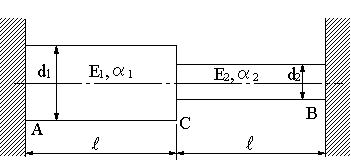
| 【問題234】 | 図のように剛体壁で両端を固定されている直径d1と直径d2の丸棒の場合に温度をΔT上昇させた場合に次の値を求める。 Eは弾性係数、αは線膨張係数である。 ・自由熱膨張の場合に、各材料の伸び、δ1,δ2を求める。 ・C点の移動距離δcを求める。 ・両材に生ずる応力σ1、σ2を求める。 |
||||
 |
|||||
| 【問題235】 | 【解答例】 |
||||
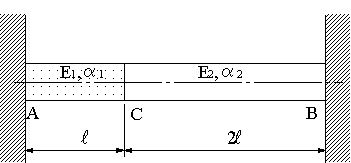
| 図のように断面積AのAB,BCの棒が接合され、A,B端で固定されている。角棒の弾性係数、線膨張係数は、図に示すようにE1,E2,α1,α2である。長さはL, 2Lである。温度がΔT上昇させたときに次の値を求める。 ・自由膨張の場合のABの膨張量を求める。 ・AB,BCに生ずる応力とひずみを求める。 ・A,B点における固定端に及ぼす反力を求める。 ・C点の移動量を求める。 * 1>>αΔT,∴1+αΔT≒1として計算しても良い。 |
|||||
 |
|||||
| 【解答例】 |
|||||
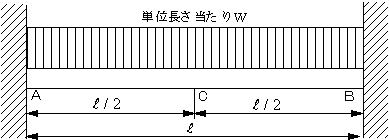
| 【問題236】 | 図の梁の場合に、曲げモーメント図とC点におけるたわみを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
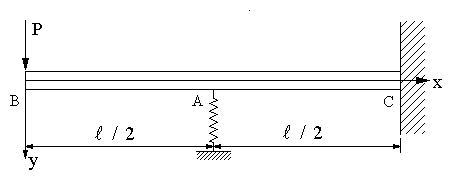
| 【問題237】 | 図のように片持ちばりの自由端Bに荷重Pが作用し、A点でバネ定数kのバネに支えられている。梁の弾性係数E、断面二次モーメントをIとして、A点に作用するバネの反力を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
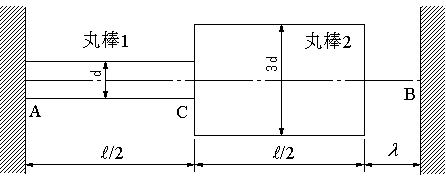
| 【問題238】 | 図のように長さがl/2で、直径がdと3dの丸棒が連結されて、左端は剛体壁に固定され、右端は剛体壁とλの隙間がある。この状態でC点にCB方向のFの大きさの荷重を作用させ、3dの丸棒の右端を剛体壁に接触させる。左右の剛体壁に生ずる反力PlとPrを求める。弾性係数は両材ともEとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 【問題239】 | 同一の断面積を持つ、同一素材の中空軸と中実軸があり、トルクTが作用している。 中空軸の内外径の比は0.5のとき、最大せん断応力は中空軸のほうが低くなるが、中実軸の最大せん断応力の何%低減するかを求める。中実軸の外径をd、中空軸の外径をdo内径をdiとする。 |
||||
| 【解答例】 |
|||||
| 【問題240】 | 高さがH、断面積Aの棒がつるされている。この棒に重りPが作用しているとき、棒の自重による伸びが重りによる伸びに対して、1%以内なら自重を無視して考えたい。棒の密度をρとして棒の重さに対して錘は何倍以上ある必要があるか。棒の縦弾数係数をEとする。 | ||||
| 【解答例】 |
|||||
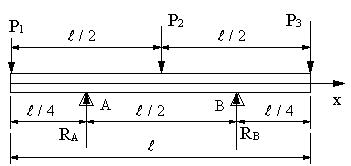
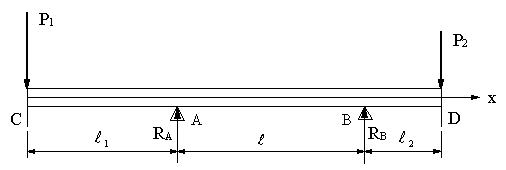
| 【問題241】 | 図に示すような両側にl1、l2の張り出しをもつ両端突出はりがある。ただし、P1>P2、l1>l2とし、xはC点を原点に取る。 ①CA間、AB間、BD間のせん断力Vx、曲げモーメントMxを求める。 ②最大曲げモーメントMmaxと、Mmaxが生ずる位置(Cより右向きにとる)を求める。 ③SFD及びBMDを描く。 ④はりの断面は一様で、高さhが幅bの√2倍の長方形とすると、b,hはいくらに取れば安全か。ただし、P1=2000N、 P2=1500N、l1=200㎜、l2=100㎜、l=300㎜、σa=80MPaとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
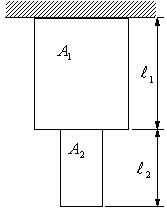
| 【問題242】 | 図のように段付きの断面積がA1,A2、長さl1,l2の棒の上端が固定されている。自重による全体の伸び量を求める。密度はいずれもρ、ヤング率Eで、重力加速度gとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
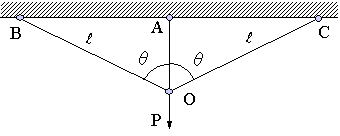
| 【問題243】 | 図のような不静定トラス構造の点Oに鉛直方向にPの荷重が作用する場合に、部材OAの伸びを求める。部材OBと部材OCの長さは等しく、部材OAとのなす角はθとし、いずれの部材も断面積と弾性係数はA、Eである。 |
||||
 |
|||||
| 【解答例】 |
|||||
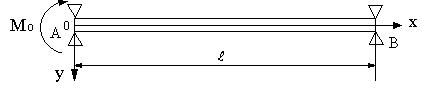
| 【問題244】 | 図のように、単純支持はりのA点にモーメントMoが作用するときの両支点の反力とたわみ角、たわみの式を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
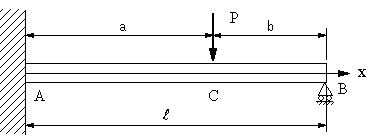
| 【問題245】 | 図の梁の場合にせん断力図、曲げモーメント図、たわみの式を求める。弾性係数E、断面二次モーメントIとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
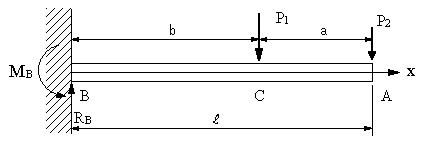
| 【問題246】 | 図の片持ち梁の場合に、B点に生ずる反力とモーメントを求め、せん断力、曲げモーメントを求め、せん断力図と曲げモーメント図を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
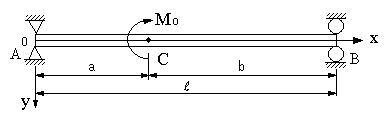
| 【問題247】 | 図の梁の場合のたわみ角、たわみの式を求める。さらに、C点のたわみ角、たわみを求める。梁の断面二次モーメントI、ヤング係数Eとする。 | ||||
 |
|||||
| 【解答例】 |
|||||
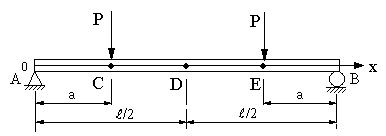
| 【問題248】 | 図のような両端支持はりについて、中央の点Dにおけるたわみを、カスチリアーノの定理を用いて求める。 せん断による変形は無視し、曲げ剛性はEIとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
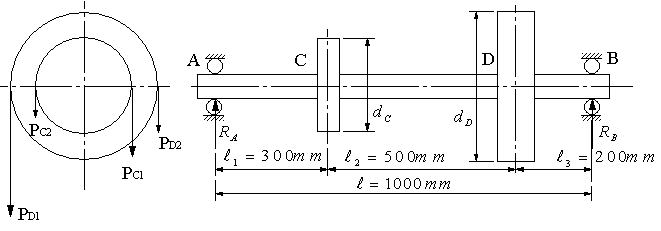
| 【問題249】 | 図に示す軸AB上の点C、DにVベルト車が付いていて、直径dC=200mm,dD=400mm,Vベルトの張力はPC1=1600N,PC2=100N,PD1=800N,PD2=50Nである。 支点A,Bに働く反力RA,RBを求め、軸CDに作用するねじりモーメントTとSFD、BMDを求める。最大曲げモーメントMを求め、軸の許容曲げ応力σa=60MPa、許容ねじり応力τa=40MPaの材料として、安全な軸径dを求める。 |
||||
 |
|||||
| 【解答例】 |