| 材料力学におけるミスの少ない計算例 | |
| 応力の単位は、SI単位では[N/m2]で表示されるが、材料力学では一般に小さすぎる単位であるので、MPa(×106)、GPa(×109)が使用される。以前は、工学単位が使われていたが、[kgf/mm2],[kgf/cm2]等である。力の単位としては、[kN], [N]よりも、日常的に使用されている[kgf]、[tonf]が大きさとしては感覚的に解りやすい。 学生さんの回答など採点していますと、0の数の間違い、単位換算の際のミスなど多く見られます。おそらく、電卓での0の数の打ち間違いから、発生すると思います。数値は、仮数部と指数部に分解して、指数部は、暗算で計算し、電卓では計算しないようにしています。単位変換の際、ミスが生ずる確率が高いので、「はじめての材料力学」(小山、鈴木著、森北出版)では、単位変換の必要がない、力[N]、長さ[mm], 応力[MPa]を推奨している。 ここでは、「はじめての材料力学」では詳細に解説しているミスのない計算の仕方の一部を述べます。 *以下の計算例では、計算を簡略化するために、有効数字は考慮しておりません。有効数字を考慮する必要がある場合は、最終結果は有効数字の丸め方に従ってください。そのため、途中の計算では与えられた数値を四捨五入の処理はしないようにすることが必要です。有効数字の扱い方については、このページをご覧下さい。 |
|
| 【問題】 | 直径5.0㎝,長さ2.00mの鋼製丸棒をその軸方向に荷重98kNの力で引張るときに生ずる応力σMPa,ひずみε%,伸びΔLmmを計算せよ。ただし,鋼のヤング率をE = 20.6×104MPaとする. |
| 【解答】 | 直径do=5.0㎝,長さL=2.00m,荷重P=98kN、丸棒の断面積Aoと置く。 断面積Ao=πdo2/4 |
| 応力σは となる。 |
|
| σの式に、do= 5.0㎝= 50mm= 5×10mm, P= 98kN= 9.8×104Nを代入 |
|
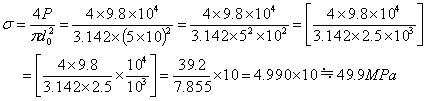 *[ ]の部分は省略可能 *[ ]の部分は省略可能 |
|
| 伸びΔLは、フックの法則から | |
| |
|
| 上式に、do= 5.0㎝= 50mm= 5×10mm,P= 98kN= 9.8×104N、L= 2.00m= 2.00×103mm 、 E= 20.6×104MPa= 2.06×105 MPa を代入 |
|
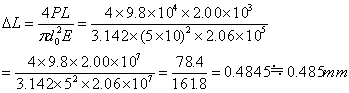 |
|
| ひずみεは定義から次式となる。 | |
| |
|
| 上式に、伸びΔL=0.4845mm, L= 2.00m= 2.00×103mmを代入する。 | |
| |
|
| *ひずみの計算は次式でも良い。 | |
| |