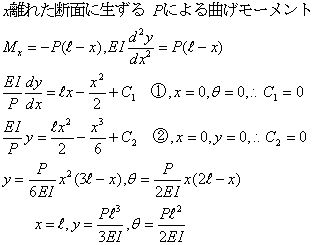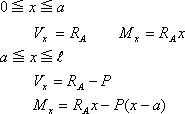|
はりの解析に定義した値、符号、座標軸の取り方等について
|
|
日本の材料力学の教科書をみると、x軸の取り方が様々である。「はじめての材料力学」では、
S.Timoshenko and D.H.Young, 「Elements of Stremgth of Materials」の教科書に従った。多くの教科書はこの著名な教科書に従っている場合が多い。座標の取り方が、3つのケースが存在する。学生にとっては教科書が違った場合、混乱が生じている場合があると思われる。これらの座標の取り方と解法について解説する。
|
| (1). |
「はじめての材料力学」、S.Timoshenko and D.H.Young, 「Elements of Stremgth of Materials」の場合 CASE 1 |
|
両端支持の場合は変わりはないが、片持ちばりの場合、自由端をx軸の原点に取っている。この場合は、長さxのはりのmn断面に生ずるせん断力Vx、曲げモーメントMxを求めることになる。 |
|
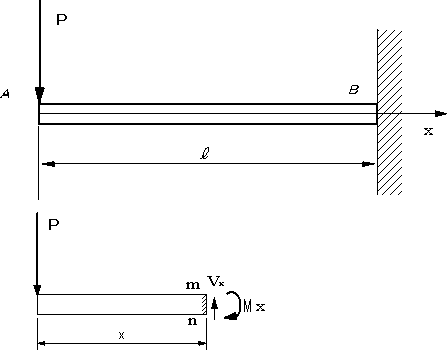
図1自由端をx軸の原点に取る場合
|
|

|
| (2). |
固定端をx軸の原点に取っている場合。 CASE 2 |
|
この場合は、固定端に生ずる反力RAとモーメントを計算して求める。図2の場合はRA=P, MA=-Plとなる。この場合は、集中荷重が一つで、簡単であるが、等分布荷重など加わった場合、複雑な荷重の場合などはRA、MAの計算が複雑となる。せん断力、曲げモーメントも符号の定義も教科書によって異なる。
|
|
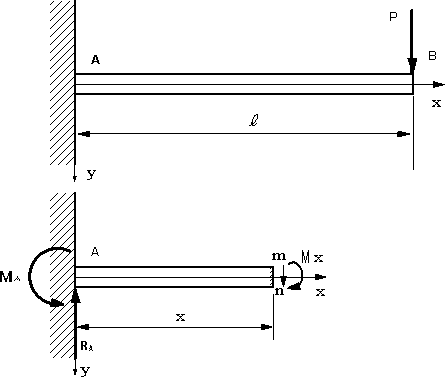
図2.固定端をx軸の原点に取っている場合
|
|
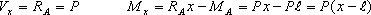
|
| (3). |
固定端をx軸の原点に取っている場合 その2 CASE 3 |
|
固定端をx軸の原点に取り、(L-x)の長さのはりBCに着目して計算する場合もある。結果は同じでも、理解しにくい所がある。
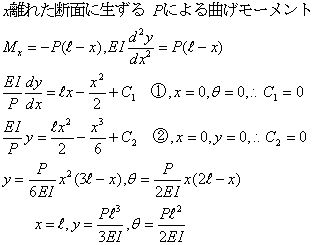
|
|
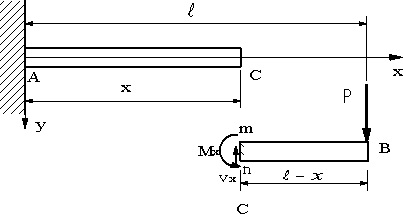
図3 |
| ■ |
せん断力Vx、曲げモーメントMxの符号について |
|
小山、鈴木著、「はじめての材料力学」、森北出版では次のように、せん断力Vx、曲げモーメントMxの符号を定義している。S.Timoshenko
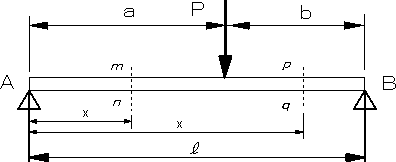
and D.H.Young, 「Elements of Stremgth of Materials」の場合とおなじである。これについても、教科書により異なるのが実情である。単純支持、集中荷重の図4の場合に、断面mn,断面pnのせん断力Vx、曲げモーメントMxを求める。
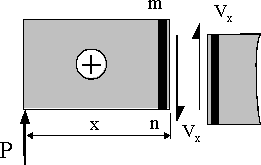
せん断力Vxについては、A端からxの距離にあるmn断面に生ずる値を求める。図5(a)のように、集中荷重Pが上向きに作用するとき、mn断面には集中荷重Pと釣り合うためのPとは向きが反対の下向きのVxが生ずる必要がある。これがせん断力Vxである。たわみを求めるときなど、y座標を下向きを+方向に取るため、この方向のせん断力を+と定義する。言い方を変えると、考えているxのはりの長さの部分を下から上に持ち上げるような場合を「+」,反対方向の場合を「−」と定義する。
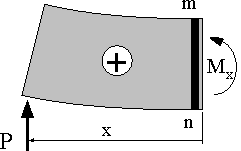
曲げモーメントMxに付いては、図6(a)の場合、集中荷重Pはmn断面上の点に関して、考えているxのはりの長さの部分を時計方向に回転させるモーメントPxを与える。これと釣り合うためには断面上の点に関して、反時計方向に回転させるモーメントMxが生ずる必要がある。これが曲げモーメントMxである。この方向の曲げモーメントを「+」、反対方向を「−」と定義する。別の言い方では、はりを下に凸に変形させるモーメントの場合「+」、上に凸の場合を「−」と定義する。 |
|
|
図4 両端支持、集中荷重のはり
|
|
|
 |
 |
| (a) Pはxの部分のはりを上に上げる作用 |
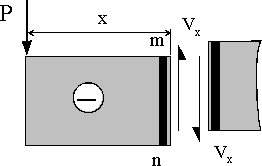
(b) Pはxの部分のはりを下に下げる作用 |
図5 せん断力Vxの符号
|
|
 |
 |
| (a) Pは下に凸に変形させるように作用 |
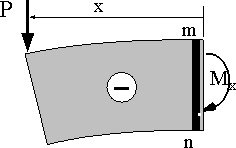
(b) Pは上に凸に変形させるように作用 |
図6 曲げモーメントMxの符号
|
|
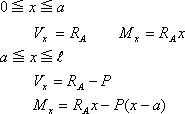
|
|
せん断力Vx、曲げモーメントMxの符号も上に述べた場合と全く逆に定義している教科書もあり、教科書が違うと、座標の取り方、せん断力Vx、曲げモーメントMxの符号の定義が異なっていて、学生は混乱すると思われる。
小山、鈴木著、「はじめての材料力学」、森北出版では、" 日本の教科書の原本"と言われているS.Timoshenko and D.H.Young, 「Elements of Stremgth of Materials」と同じように定義している。
|
| ■ |
等分布荷重の扱い 小山、鈴木著、「はじめての材料力学」、森北出版 |
|
等分布荷重は、分布の中心に分布の合力が作用するとして扱うと力学的に同等になる。このように置き換えると支点の反力を力の釣り合い、モーメントの釣り合いから求める場合に簡略化できる。
|
| |
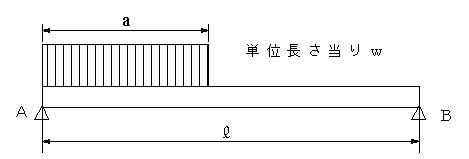
図7
|
| |
図の場合に、支点の反力RA,RBは図8のように、分布荷重を分布の中心a/2に合力waが集中荷重として作用すると置き換えると簡単に計算できる。RA+RB-wa=0, -RAL+wa(L-a/2)=0 |
| |
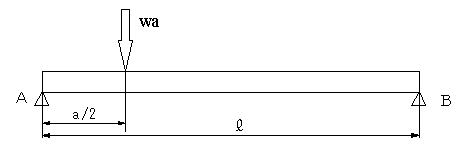
図8
|
| ● |
せん断力や曲げモーメントの計算 |
|
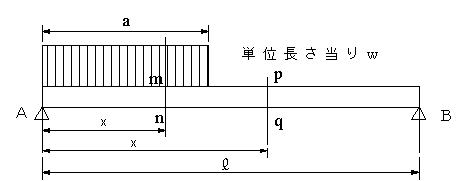
図9 |
|
0<x<aの時 図10のように集中荷重wxがx/2に作用するとして、Vx=RA-wx、Mx=RA・x-wx・x/2=RA・x-wx2/2
|
|
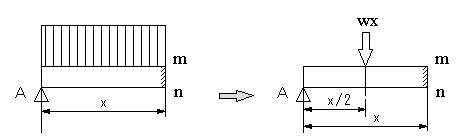
図10 |
|
a<x<Lのとき、図11のように集中荷重waがa/2に作用するとして,Vx=RA-wa、Mx=RA・x-wa(x-a/2)
|
|
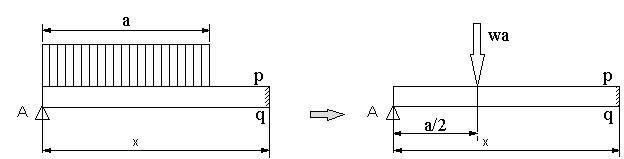
図11 |