| 【問題151】 |
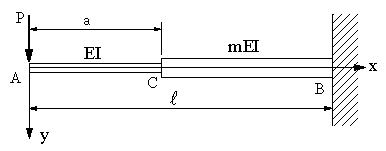
図のような片持ちばりで、先端からaまでは、曲げ剛性がEI,aからLまでがmEIのとき、自由端におけるたわみと、たわみ角、たわみの式を求める。を求める。
|
|
|
|
【解答例】
|
| 【問題152】 |
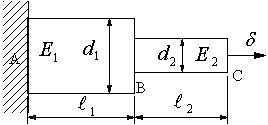
Aで固定され、直径とヤング率と長さが異なる棒を図のように組み合わせた棒のC面に荷重を加え、δだけ変位させた。このときの各棒に生じる各部の応力とひずみを求める。ただし、各部材の弾性係数をE1,E2とする。
|
|
|
|
【解答例】
|
| 【問題153】 |
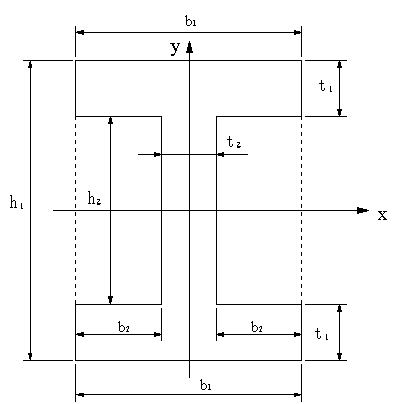
図において、長さ5mのI形鋼を単純支持ばりとして用いたとき、はりに働いている重力によるたわみを求める。ただし、鋼材の単位当たりの質量を7.85×10-6kg/mm3、縦弾性係数を206GPaとする。b1=75mm,t1=8mm,t2=5mm, h1=100mm, h2=84mm
|
|
|
|
【解答例】
|
| 【問題154】 |
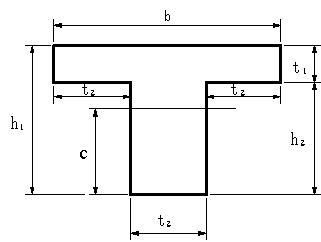
図の図心と、断面二次モーメント、断面係数を計算する。ただし、 b=60mm,t1=10mm,t2=20mm, h1=40mm,h2=30mmとする。
|
|
|
|
【解答例】
|
| 【問題155】 |
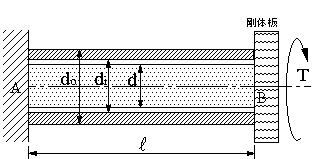
図のような、長さL、外径do、内径diのパイプの中に、同一部材の直径dの丸棒が挿入されており、A端は壁に固定され、B端に剛体板が取り付けられている。この剛体板にねじりモーメントTが作用しているとき、以下の問に答えよ。ただし、パイプ、丸棒の横弾性係数はGとする。
(1).パイプと丸棒に作用するねじりモーメントTH,TSを求めよ
(2).パイプと丸棒の最大せん断力τH、τSを求めよ。
ただし、L=600mm, do=75mm,di=65mm,d=50mmT=2kN・m,G==80GPaとする。
(3).ねじり角φを求める。 |
|
|
|
【解答例】
|
| 【問題156】 |
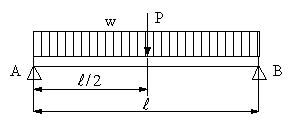
両端支持、長さが10m、幅3.8m橋桁の中央に集中荷重1400kgと自重が作用する場合に、安全な長方形断面の橋桁の高さhを求める。橋桁の材料の密度7.8g/cm3、降伏応力260MPa、安全係数4.5とする。
|
|
|
|
【解答例】
|
| 【問題157】 |
回転数300rpmで55馬力を伝える伝動軸の安全な直径を求める。ただし、軸の許容せん断応力を200MPaとし、ねじれ角が1mあたり1/4°以下とする。横弾性係数はG=79.2GPaとする。
|
|
【解答例】
|
| 【問題158】 |
体積率30%のガラス繊維で軸方向に連続繊維で強化した複合材料において、ガラス繊維の弾性係数は68GPa、マトリックス相であるポリエステルレジンの体積率は70%である。硬化したときの弾性係数を4.4GPaとする。 |
|
| (1) |
この複合材料の縦方向の弾性係数を求める。 |
| (2) |
複合材の断面積を250mm2とするとき、軸方向に50MPaの応力が生じている。繊維とマトリックスのそれぞれに負荷されている荷重を求める。 |
| (3) |
(2)の応力が生じているとき、ガラス繊維と母材に生じているひずみを求める。 |
|
|
【解答例】
|
| 【問題159】 |
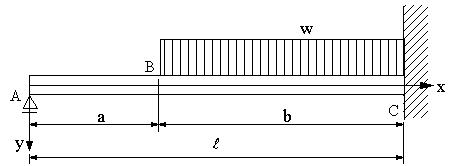
図の不静定の梁の場合に、たわみ曲線とA支点の反力を求める。
|
|
|
|
【解答例】
|
| 【問題160】 |
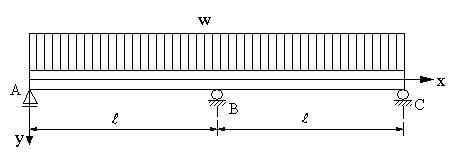
図の不静定梁の場合に、各支点における反力とたわみの式を求める。
|
|
|
|
【解答例】
|
| 【問題161】 |
長さ400mmの単純支持はりの中央に集中荷重Pが作用する。はりは、図のようなH型鋼で、許容曲げ応力が
80MPaのとき、安全な荷重の大きさを求める。ただし、b=50mm,h=60mmm,t1=10mm,t2=20mmである。
|
|
|
|
【解答例】
|
| 【問題162】 |
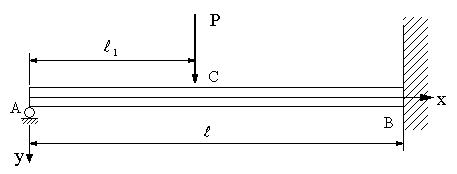
図の梁の場合、たわみ曲線とB,Cにおける曲げモーメントを求める。
|
|
 |
|
【解答例】
|
| 【問題163】 |
直径d(半径r)の円形断面の断面二次モーメントと断面二次極モーメントの計算
|
|
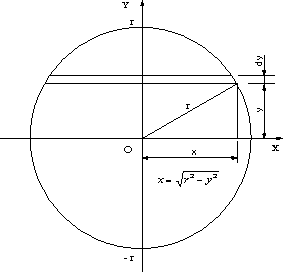
|
|
【解答例】
|
| 【問題164】 |
図に示す厚さtの台形板に引張荷重Pが作用した場合に生ずる伸びを求める。ただし、ヤング係数をEとする。
|
|
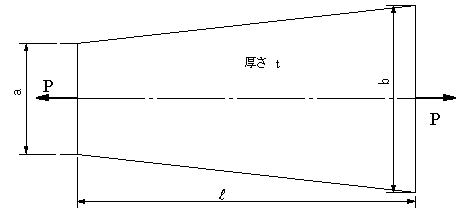
|
|
【解答例】
|
| 【問題165】 |
図の直径dの片持ちばりの場合に、
(1).最大曲げモーメントと生ずる最大応力を求める。
(2).たわみ曲線を求める。断面二次モーメントI、ヤング率Eと置く。
(3).C点におけるたわみ角とたわみを求める。
(4).最大たわみを求める。 |
|
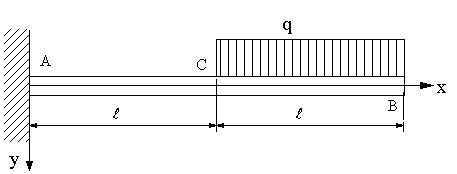
|
|
【解答例】
|
| 【問題166】 |
図の片持ち梁は直径dと2dからなる丸棒で,縦弾性係数E,断面二次モーメントIである。
(1).点Aに生じる反力と曲げモーメントを求める。
(2).点Aに生じる最大曲げ応力を求める。
(3).点Cのたわみとたわみ角を求める。
(4).点Bのたわみを求める。
|
|
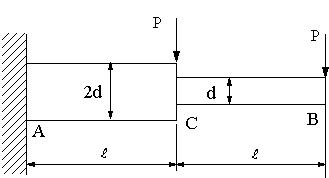
|
|
【解答例】
|
| 【問題167】 |
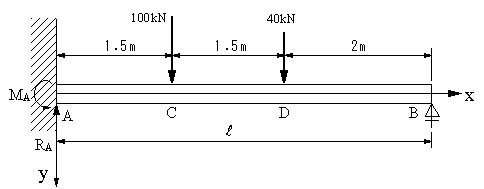
図の場合の梁において、A,B点における反力、A点におけるモーメントを求める。次に、たわみ曲線を求める。弾性係数E,断面二次モーメントIとする。
|
|
|
|
【解答例】
|
| 【問題168】 |
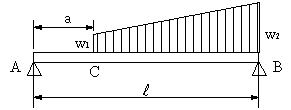
図の場合のせん断力と曲げモーメントを求める。 |
|
|
|
【解答例】
|
| 【問題169】 |
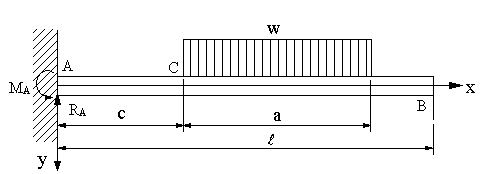
図の片持ちばりの場合にたわみの式と最大たわみを求める。
|
|
|
|
【解答例】
|
| 【問題170】 |
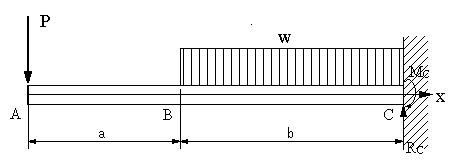
図の梁の場合にC点の反力とモーメントを求める。そして、せん断力と曲げモーメントを求め、せん断力図と曲げモーメント図を示す。 |
|
|
|
【解答例】
|
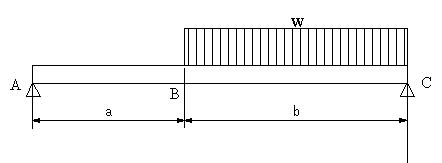
| 【問題171】 |
図の梁の場合に、せん断力と曲げモーメントを求め、せん断力図と曲げモーメント図を示す。
|
|
|
|
【解答例】
|
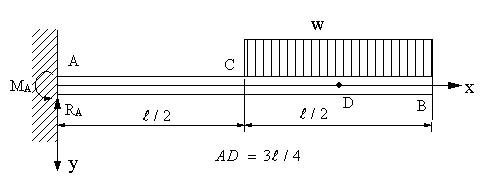
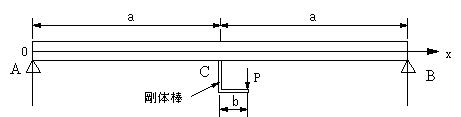
| 【問題172】 |
図の梁の場合にせん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。断面係数Z=bh2/6
として、最大応力の値を求める。
|
|
 |
|
【解答例】
|
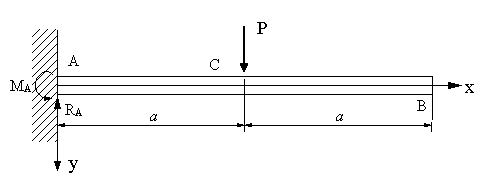
| 【問題173】 |
図の梁の場合に、たわみ曲線と自由端におけるたわみを求める。
|
|
|
|
【解答例】
|
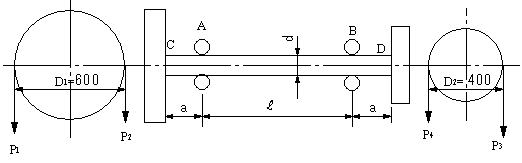
| 【問題174】 |
図のように、両端に直径600㎜及び400㎜のプーリーを有する直径40㎜の軸がA、Bでベアリングで支持され、プーリーには、P1,P2,P3,P4の力が作用している。軸に生じる最大曲げ応力と最大剪断応力とを求める。ただし、P1=2[kN],P2=1[kN], P3=1.5[kN],P4=1[kN]である。
|
|
 |
|
【解答例】
|
| 【問題175】 |
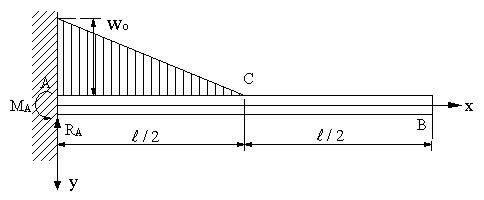
図の片持ち梁の場合にたわみの式を求める。
|
|
|
|
【解答例】
|
| 【問題176】 |
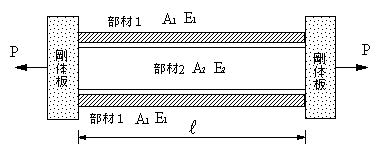
図に示すように2本の部材1と1本の部材2の両端が固定され、荷重力Pが作用する時、各部材の伸び、生ずる応力を求めよ。ただし、それぞれの部材の縦弾性係数をE1,E2、断面積をA1,A2とする。
|
|
|
|
【解答例】
|
| 【問題177】 |
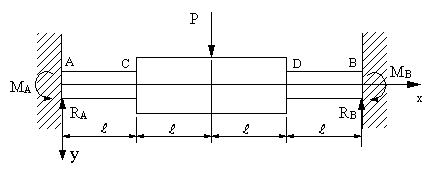
図の梁の場合に、たわみの式と、最大たわみを求める。 AC,DB部分の梁の断面二次モーメントI1,とし、CD部分の梁の断面二次モーメントI2とし、弾性係数はいずれもEである。
|
|
|
|
【解答例】
|
| 【問題178】 |
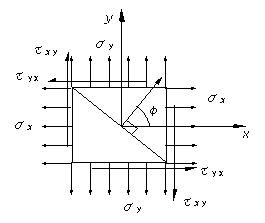
図のように、平面応力状態でσx=-60MPa,σy=40MPa,τxy=10MPaが作用するとき、主応力の大きさとその時の角度、最大せん断応力とその時の角度を求める。 |
|
|
|
【解答例】
|
| 【問題179】 |
長さ150mm、直径10mmnのアルミニウムの円柱を片側固定して、固定端を軸とし、2000rpmで回転させたとき、回転軸からx=10mmの断面に生ずる応力と、回転する棒の伸びを求める。アルミニウムのヤング率69GPa,密度を2.7×103[kg/m3]とする。
|
|

|
|
【解答例】
|
| 【問題180】 |
図の梁の場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図を求める。
|
|
|
|
【解答例】
|
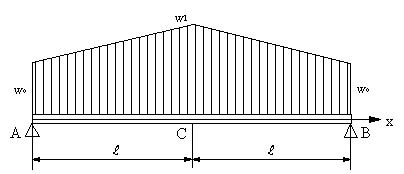
| 【問題181】 |
図のような分布荷重が作用する両端支持はりの場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図、最大応力を求める。断面係数はZとする。
|
|
|
|
【解答例】
|
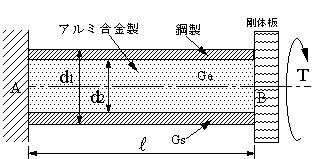
| 【問題182】 |
図のように、長さL=0.8m,外径d1=60mm,内径d2=50mmの鋼製のパイプと直径d2のアルミ合金の丸棒で製作された複合軸がある。鋼管、アルミ丸棒の許容せん断応力はそれぞれτs=140MPa,τa=70MPaで、せん断弾性係数はGs=80Gpa,Ga=28GPaとする。負荷できる最大トルクTmaxを求めよ。
|
|
|
|
【解答例】
|
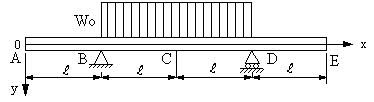
| 【問題183】 |
図のような等分布荷重がBD間に作用する梁の場合に、AD間のたわみの式とA点、C点におけるたわみを求める。なお、弾性係数E、断面二次モーメントIとする。
|
|
|
|
【解答例】
|
| 【問題184】 |
図の不静定張りの場合に、たわみ角とたわみの式、各支点の反力、せん断力図、曲げモーメント図を求める。
|
|
|
|
【解答例】
|
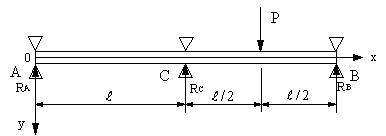
| 【問題185】 |
図の不静定梁の場合に、たわみ角とたわみの式、各支点の反力、せん断力図、曲げモーメント図を求める。
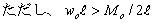
|
|
|
|
【解答例】
|
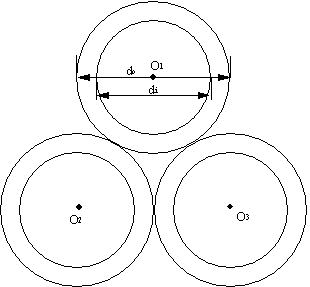
| 【問題186】 |
外径do,内径diの3本の中空軸を図のように接着した梁の場合の図心の位置と断面二次モーメントを計算する。
|
|
|
|
【解答例】
|
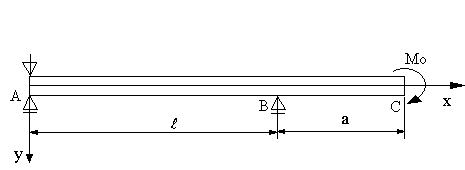
| 【問題187】 |
図の両端支持ばりの場合に,たわみ角の式、たわみの式とC点におけるたわみを求める。
|
|
|
|
【解答例】
|
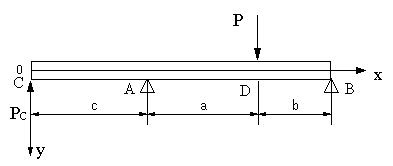
| 【問題188】 |
図の梁の場合に、せん断力、曲げモーメント、たわみ角の式、たわみの式を求める。
|
|
|
|
【解答例】
|
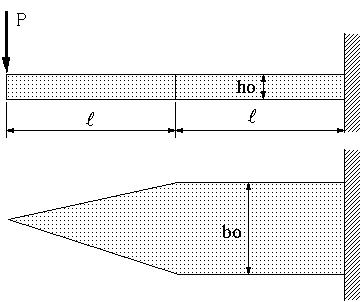
| 【問題189】 |
図のように、厚さhoが一様で,幅が異なる片持ちばりの場合に自由端のたわみを求める。
|
|
|
|
【解答例】
|
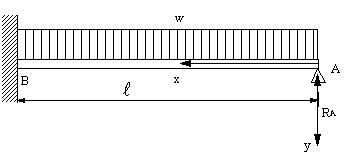
| 【問題190】 |
図の不静定梁の場合にもせん断力、曲げモーメントを求め、せん断力図、曲げモーメント図を描く。最大な曲げ応力とせん断応力を求め、また、たわみ角、たわみ曲線を求める。
|
|
|
|
【解答例】
|
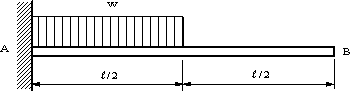
| 【問題191】 |
図の梁の場合に、自由端におけるたわみ角とたわみを求める。
|
|
 |
|
【解答例】
|
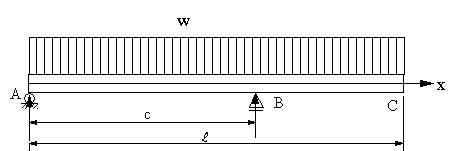
| 【問題192】 |
図の梁の場合に、AB部の曲げモーメントの最大値とBC部の曲げモーメントの最大値が同じくなるcの値を求め、その時のせん断力図と曲げモーメント図を求める。 |
|
|
|
【解答例】
|
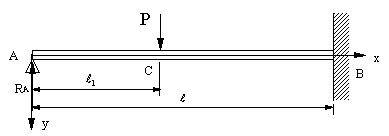
| 【問題193】 |
図の梁の場合に、A支点の反力とたわみ曲線を求める。
|
|
|
|
【解答例】
|
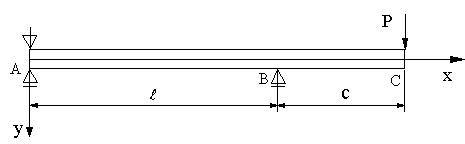
| 【問題194】 |
図の梁の場合に、たわみ角の式、たわみの式、B,C点におけるたわみ角とC点のたわみを求める。
|
|
|
|
【解答例】
|
| 【問題195】 |
軸にトルクが作用するトルク場合の軸径の設計 |
| (1). |
回転速度N=500rpmで動力P=4.5kWを伝達する安全な中実丸軸の直径d(㎜)を強度と剛さの両面から決定する。
ただし、軸の許容比ねじれ角は1mあたり0.25度以下とし、軸の材料は軟鋼、許容せん断り応力τa=50MPa、横弾性係数G=80GPaとする。 |
| (2). |
回転数1500rpmで動力が80kWを伝えるのに強度的に安全な円筒軸の内径及び外径を求める。
ただし内外径比をm=di/do=0.7 横弾性係数G =81GPa 許容比ねじれ角0.002rad/m 許容せん断応力12MPaとする。
|
|
【解答例】
|
| 【問題196】 |
図のように、断面積A1の円筒の中に、断面積A2の中実丸棒を温度T1で剛体板で接合した。その後、温度T2(T2>T1)を変化させたときに、熱応力によって両材に生ずる応力、σ1とσ2を求める。T1の時の初期長さlo、線膨張係数 α1,α2(α1<α2),ヤング率 E11、E2とする。
|
|
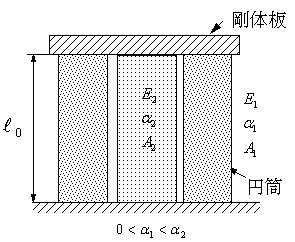 |
|
【解答例】
|
| 【問題197】 |
図の梁の場合に、曲げモーメントとたわみを求める。
|
|
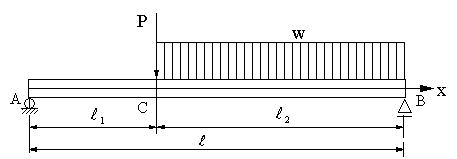
|
|
【解答例】
|
| 【問題198】 |
図の梁の場合に、せん断力と曲げモーメントを求める。
|
|
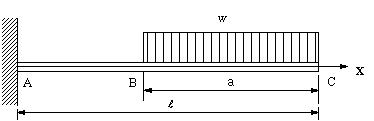
|
|
【解答例】
|
| 【問題199】 |
図の断面二次モーメントを求める。
|
|
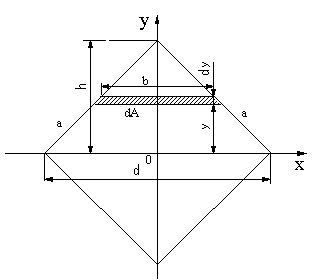
|
|
【解答例】
|