| 材料力学の典型的な問題 PartⅡ |
|
「はじめての材料力学」で提案している材料力学における「ミスの少ない計算」については、こちらをご覧下さい。 片持ちばりの座標軸の取り方についてはこちらをご覧下さい。 |
 |
「はじめての材料力学」サポートページ >材料力学の典型的な問題 PartⅡ
| 材料力学の典型的な問題 PartⅡ |
|
「はじめての材料力学」で提案している材料力学における「ミスの少ない計算」については、こちらをご覧下さい。 片持ちばりの座標軸の取り方についてはこちらをご覧下さい。 |
 |
| 【問題51】 | 外径do、内径diの中空軸に、ねじモーメントTが働いている。材料の横弾性係数をGとする。以下を求めよ (1).この軸の断面2次極モーメントJ を求める。 (2).任意の半径rの位置に生ずるねじり応力τと最大ねじり応力 τmaxを求める。 (3).単位長さ当たりのねじれ角θを求める |
||||
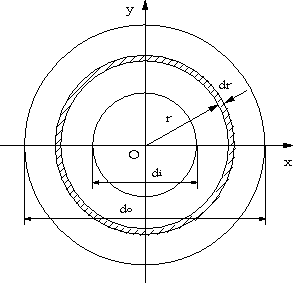 |
|||||
| 【解答例】 |
|||||
| 【問題52】 | 直径d=5m、長さL=10m、肉厚t=25mmの閉じた薄肉円筒がある。円筒中央の外側の表面で接線方向とθ=45°をなす方向の垂直ひずみを測定したところ,ε=0.001であった。この薄肉円筒の内圧pを求めよ。 ヤング率E=206GPa
とする。 |
||||
| 【解答例】 |
|||||
| 【問題53】 | 剛性板を介して荷重Pの作用する鉄筋コンクリートの円柱がある。 鉄筋部とコンクリート部の総断面積をそれぜれAs=500mm2、Ac=6000mm2、鉄筋とコンクリートの圧縮許容応力をそれぞれσs=150MPa、σc=10MPaとする。なお、鉄筋とコンクリートの弾性係数をそれぞれEs=206GPa, Ec=20.6MPaとする。 |
||||
| (1). | 円柱のひずみεoとして、荷重との関係式を求める。 | ||||
| (2). | 鉄筋とコンクリートがそれぞれ、単独に負荷されたとき、フックの法則から許容応力に対応するそれぞれのひずみεs,εcを計算し、鉄筋コンクリートの円柱に生ずる安全なひずみεoを求める。 | ||||
| (3). | .安全に負荷できる荷重Pの最大値はいくらになるか。 |
||||
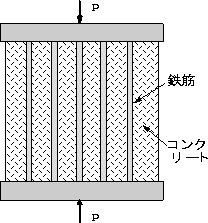 |
|||||
| 【解答例】 |
|||||
| 【問題54】 | 図のような直径d1,右半分が直径d2=1.414d1のはりの場合に、自由端におけるたわみを計算する。 |
||||
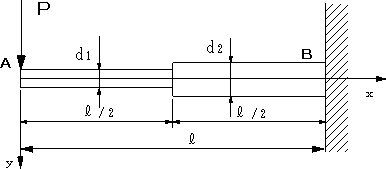 |
|||||
| 【解答例】 |
|||||
| 【問題55】 | A点からC点までw=6kN/mの等分布荷重が作用し、D点にP=10kNの集中荷重が作用する両端支持はりのとき、せん断力図、曲げモーメント図、曲げモーメントの最大値が生ずる位置と最大値を求める。 |
||||
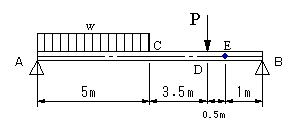 |
|||||
| 【解答例】 |
|||||
| 【問題56】 | 断面積A、長さ2Lの棒が、棒の中心を通る軸の周りにNrpmで回転している。中心からxの距離にある断面に作用する遠心力と応力を求め、応力の最大値を求める。単位体積当たりの重量wとする。 |
||||
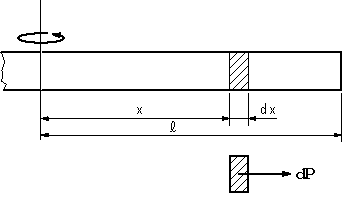 |
|||||
| 【解答例】 |
|||||
| 【問題57】 | 図のはりの場合、P=1000Nの時、AB,BC,ACの部材に作用する荷重と支点B,Cにおける反力をを求める。 |
||||
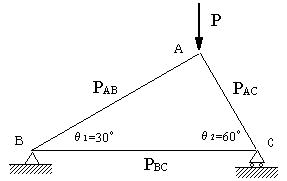 |
|||||
| 【解答例】 |
|||||
| 【問題58】 | 図のように、両端固定の段付中実丸軸で左端から段部までの長さをL, 半径を2r,
段部から右端までの長さをL, 半径をrとした時、段部から右端へL/2のC点にねじりモーメントTを与えた場合、 段部でのねじり角とそれぞれの軸に生ずるせん断応力τ1,τ2を求める。 |
||||
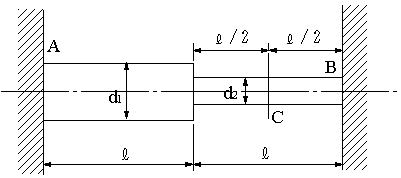 |
|||||
| 【解答例】 |
|||||
| 【問題59】 | 図のように、長さL、断面積2AのB材と、長さ2L、断面積Aの2本のC材が剛体板に固定されている。両材の線膨張係数α、ヤング係数Eとして、温度がΔT変化したとき、両材に生ずる荷重PB,PCと伸びδB,δCを求める。 |
||||
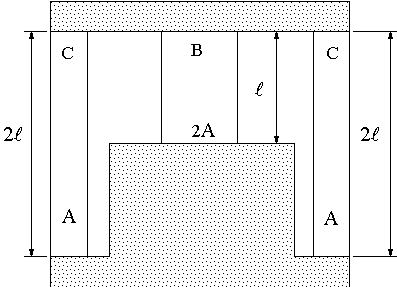 |
|||||
| 【解答例】 |
|||||
| 問題60 | 断面積の等しい中実丸棒と中空丸棒のはりに曲げモーメントを加えたとき、両軸に生ずる最大応力が等しくなるための曲げモーメントの比を求めよ。中空丸棒の内外径比は1/2とする。 |
||||
| 【解答例】 |
|||||
| 問題61 | 図のように荷重Pが作用し、はりの断面形状が図のような時、はりに生ずる曲げモーメント図と断面の図心の位置と断面二次モーメントI,断面係数Zを求め、はりに生ずる最大引張応力と最大圧縮応力を計算する。 ただし、P=4kN,はりの長さ600mm,r=h=25mmとする。 |
||||
|
|||||
| 【解答例】 |
|||||
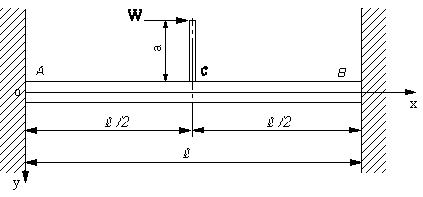
| 問題62 | 図のように両端が固定されているはりの中央に横木を固定し、はりの中心からaの位置に水平に荷重Wを加える。梁のたわみ曲線と最大たわみを求める。断面二次モーメントI、縦弾性係数Eとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
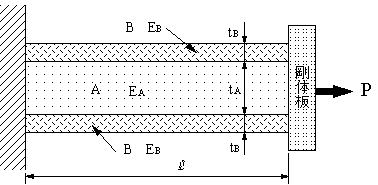
| 問題63 |
板厚tA=3.0mmのA材の両面に、板厚tB=1.0mmのB材を完全に張り合わせたサンドイッチ板があり、引張力Pがかかる。 サンドイッチ板(複合材料)の縦弾性係数Eを求める。ただし、A材は縦弾性係数EA=100kN/mm2, B材は縦弾性係数EB=5kN/mm2とする。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 問題64 | 鋼の丸棒の引張試験を行ったところ、500MPaで比例限度に達した。このとき丸棒に生じる真の応力を求めよ。ただし、縦弾性係数を206GPa、ポアソン比を0.3とする。 |
||||
| 【解答例】 |
|||||
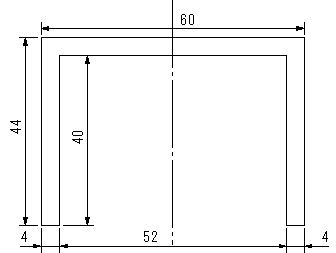
| 問題65 | 図のような断面の図心と断面二次モーメント、断面係数を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 問題66 | 直径30mmの銅製の丸棒に引張荷重Pを加えたところ、直径が0.006mmだけ小さくなった。縦弾性係数E=2.06×105MPa、ポアソン比υ=0.3としたとき、引張荷重Pの値を求めよ。 |
||||
| 【解答例】 |
|||||
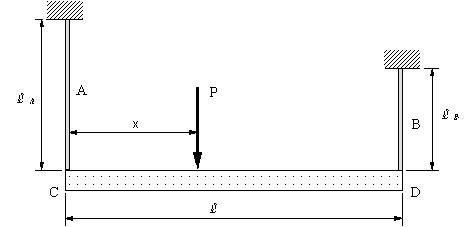
| 問題67 | 図のように、長さLA=300mm,LB=200mmのワイヤーで、剛体材CDを水平に支持する。Cから、xの位置に荷重Pを鉛直下向きに作用させたが、剛体材CDは水平を保った。xの寸法とA,B材に発生する応力がともに許容応力以下の最大荷重Pを求める。 左右のワイヤーA,Bの直径をそれぞれdA=3mm, dB=1mm,縦弾性係数の比をEA:EB = 1:3とし、許容応力をそれぞれσA=50MPa , σB=150MPaとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 問題68 | 図の両端支持はりの場合に、せん断力、曲げモーメント、最大曲げモーメントの値とそれを生じる位置を求める。ただし、L=(2/3)
L1とする。 |
||||
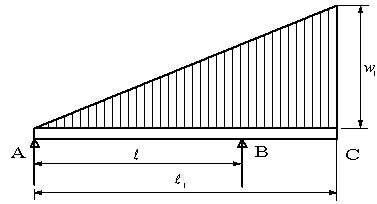 |
|||||
| 【解答例】 |
|||||
| 問題69 | 図のように、左端からaの位置に荷重分布の三角形の頂点(荷重wo)があるはりのせん断力とせん断力線図、曲げモーメントと曲げモーメント線図、最大曲げモーメントとその生ずる位置を求める。ただし、a<bとする。 |
||||
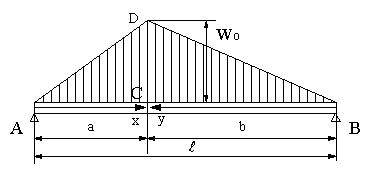 |
|||||
| 【解答例】 |
|||||
| 問題70 | 長さloの断面積A、ヤング係数Eの鋼棒を間隔lの剛体壁に固定する。lo>lである。AC=l1のC点に図(c)のように荷重Pを負荷して、BC部には負荷荷重0の状態にするとき、Pの大きさを求める。 |
||||
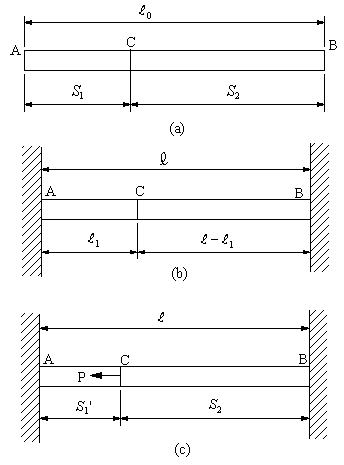 |
|||||
| 【解答例】 |
|||||
| 問題71 | 図のように剛体壁で両端が固定されている断面積A、ヤング係数Eの棒が、C、D点に荷重P1、P2を受けるとき、剛体壁A,Bが受ける反力を求める。 |
||||
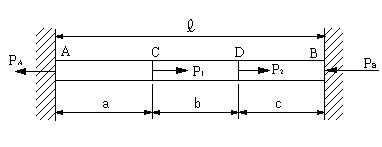 |
|||||
| 【解答例】 |
|||||
| 問題72 | 長さ1mの片持ち梁の先端に10kgの集中荷重を負荷する。はりの断面は、板厚tの、外寸法30×30mmの正方形である時、先端のたわみを10mmまで許容できるときの板厚を求める。材料はアルミニウムを使用し、ヤング係数をE=69GPaとする。この時、はりに生ずる最大応力を求める。 |
||||
| 【解答例】 |
|||||
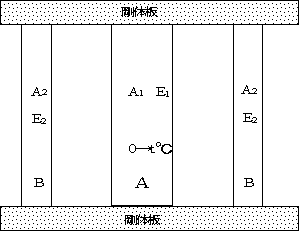
| 問題73 | 図のように、2枚の剛体板の間に材料B(縦弾性係数E2,断面積A2)2本で溶接した。その中間に材料A(E1,A1,熱膨張係数α)を入れ、Aを0℃からt℃まで加熱した時に発生する応力σ1,σ2を求めよ |
||||
 |
|||||
| 【解答例】 |
|||||
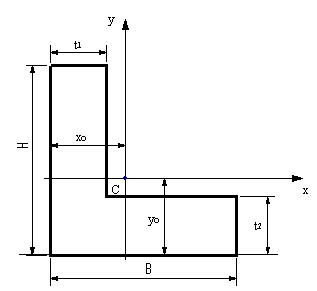
| 問題74 | 図の図心とx軸とy軸に関する断面二次モーメントを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
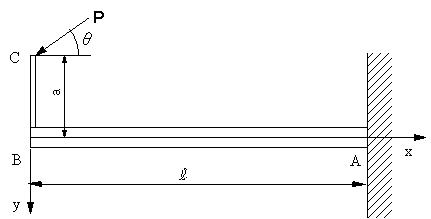
| 問題75 | 図のはりの場合に、B点のたわみと水平方向の伸びを求める。ヤング率E、断面積A、断面二次モーメントIとする。 | ||||
 |
|||||
| 【解答例】 |
|||||
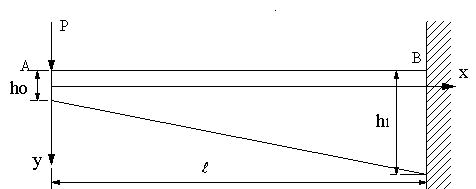
| 問題76 | 長さL、幅b,ヤング係数E,高さが図のように、hoからhlに変化する片持ち梁の場合に、自由端のたわみを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
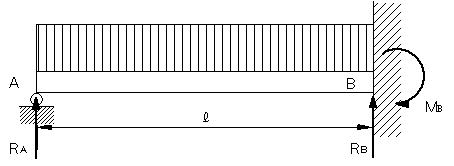
| 問題77 | 図の不静定のはりの場合のせん断力、曲げモーメント、たわみの式を求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
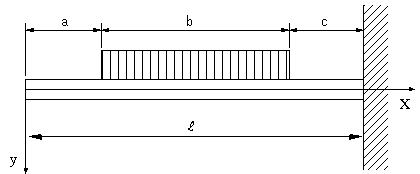
| 問題78 | 図のはりの場合に、たわみの式と自由端のたわみを求める。断面係数Z,ヤング率Eとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 問題79 | 同じ材料からなる中実軸と、外径が内径の2倍である中空軸がある。ねじりに対する強さが等しい場合の両軸の重量を比較せよ。また、横弾性係数G=8.2×104MPa、許容せん断応力τa=20MPaの材料を用いて車軸dを設計する場合に、90cmの長さについて許容される最大ねじれ角を1/4°とする。 |
||||
| 【解答例】 |
|||||
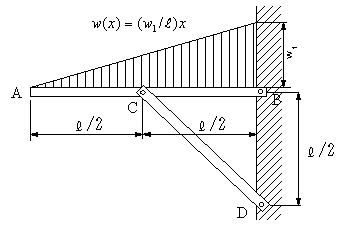
| 問題80 | 図のはりの場合にせん断力、曲げモーメントとC点に作用するはりの軸方向の荷重を計算する。B,C,D点は固定点ではなく、ピン節点とする。 | ||||
 |
|||||
| 【解答例】 |
|||||
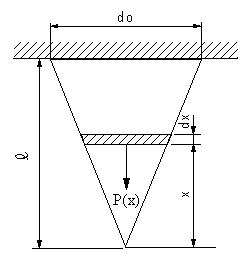
| 問題81 | 高さL,底面の直径doの円錐が底面を固定されて吊り下げられている。自重による伸びを求める。密度ρ、重力加速度gとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
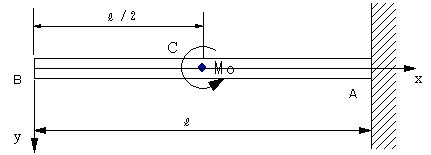
| 問題82 | 長さL,直径d,縦弾性係数をE のはりAB がある.このはりAB の端A を固定し,中点C
に反時計回りの集中偶力Mo を与えるとき,以下の設問に答えよ. (a) 長手方向の座標軸および原点を定めて,このはりに生じる曲げモーメントの式を求めよ. (b) このはりに生じる最大絶対曲げ応力およびそれが生じる位置を求めよ. (c) このはりに生じるたわみの式を求めよ. |
||||
 |
|||||
| 【解答例】 |
|||||
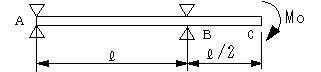
| 問題83 | 図のような両端支持はりにモーメントMoが作用している。 (a) このはりの支点における反力を求める. (b) せん断力図および曲げモーメント図を描く. (c) このはりに生じる最大曲げモーメントMmax およびそれが生じる位置を求める. (d) このはりの断面が外径d1,内径d2 の中空円筒のとき,はりに生じる最大曲げ応力σmax を求める. |
||||
 |
|||||
| 【解答例】 |
|||||
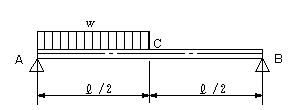
| 問題84 | 長さL のはりが両端で単純支持されている.はりの一端からL/2 にわたって等分布荷重w
が作用すしているとき,以下の設問に答えよ. (a) このはりの支点における反力を求める. (b) 長手方向の座標軸および原点を定めて,せん断力図および曲げモーメント図を描く. (c) このはりに生じる最大曲げモーメントMmax およびそれが生じる位置を求める. (d) はりの長さL = 1.00 m,断面の幅b = 27.0 mm,高さh = 10.0 mm 、等分布荷重w = 640 N/m のとき, はりに生じる最大曲げ応力σjmax を求める. |
||||
 |
|||||
| 【解答例】 |
|||||
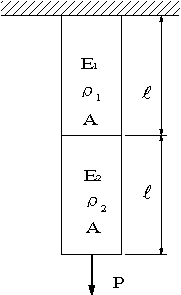
| 問題85 | 図のように長さ2Lで一様な断面積の材質の異なる棒をつるし、下端に荷重Pを加えたとき、棒の自重を考慮して棒に生じる最大応力及び棒全体の伸びを求めよ。材料Ⅰはヤング率E1、断面積A、密度ρ1とし、材料Ⅱはヤング率E2、断面積A、密度ρ2とする。重力加速度はgとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
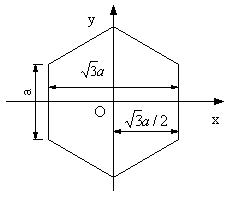
| 問題86 | 図1の正六角形断面の場合 (1) 断面2次モーメントIを求める。 (2) 断面2次極モーメントJを求める。 |
||||
 |
|||||
| 【解答例】 |
|||||
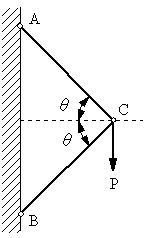
| 問題87 | 図のように、長さ750mmの2本の軟鋼棒AC、BCの両端が回転自由に結合され、C点に垂直荷重Pが作用するとき、各棒の応力およびC点の垂直変位を計算せよ。ただし、P=10kN、θ=47°、各棒の横断面積A=70mm2 、縦弾性係数E=2.06×105MPaとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
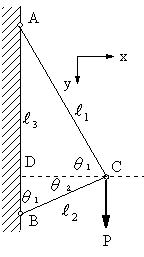
| 問題88 | 図1のように垂直な剛体壁に回転自由に取り付けられた2本の軟鋼棒AC,BCの他端C点が回転自由に結合されている。 ∠ACB=90°(θ1=60°)のとき、C点に鉛直荷重P=9.81kNを作用させたとき、C点の水平および垂直方向の変位を求める。ただし、AC,BCの線材の断面積A=200mm2,L3=2000mm,縦弾性係数E=2.06×105MPaとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
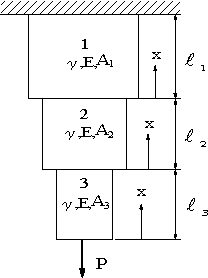
| 問題89 | 図のように、長さと断面積が異なる3つの段付き丸棒に荷重Pが作用している。各部の下面からxの距離に生ずる応力の大きさと各棒の伸び、全体の伸びを求める。密度γ、ヤング率Eとする。 |
||||
 |
|||||
| 【解答例】 |
|||||
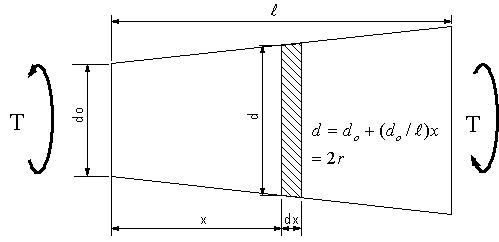
| 問題90 | 図のように、断面直径dがd=d。+(d。/L)xのように変化する長さLの軸にねじりモーメントTが作用するとき、軸に蓄えられるひずみエネルギーUを計算する。 |
||||
 |
|||||
| 【解答例】 |
|||||
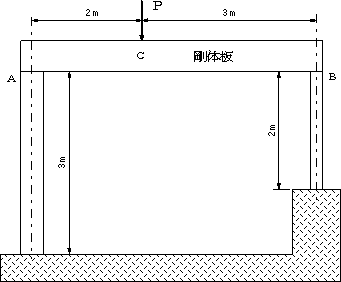
| 問題91 | 質量10kgの剛体棒が一辺30mmおよび10mmの正方形断面の棒A,Bに支えられている。剛体棒にP=1200Nの力が作用するとき、各棒に生ずる応力を求めよ。また各棒の縮み量を求めよ。ヤング率は70GPaとする。棒Aの長さは3m、棒Bの長さは2m、AからCの間は2m、棒Aから棒Bの間は5mです。
|
||||
 |
|||||
| 【解答例】 |
|||||
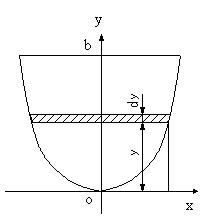
| 問題92 | 図のようなy=ax2の放物線で囲まれた断面の図心の位置と断面二次モーメントを計算する。 | ||||
 |
|||||
| 【解答例】 |
|||||
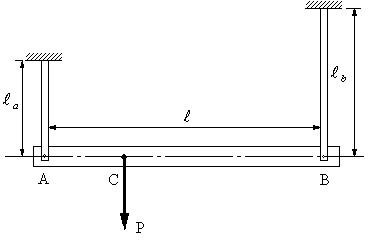
| 問題93 | 図に示すように、長さ3mの剛体の棒ABが2本の鉛直な棒の下端につるされ、水平位置を保っている。Aの棒は黄銅で長さ2m、断面積11cm2、縦弾性係数98GPa、Bの棒は 鋼で長さ3.3m、断面積5m2、縦弾性係数206GPaである。点Aからどの位置に鉛直荷重Pを加えれば、負荷後も剛体の棒ABは水平を保つか。 |
||||
 |
|||||
| 【解答例】 |
|||||
| 問題94 | 図のように長さLの両端支持はりの中央に、剛体棒を通して、長さLの片持ち梁の先端が接している。片持ち梁の先端に荷重Pが作用するとき両はりのたわみの最大値を求める。各梁の最大たわみは図1、図2の値を使用する。 |
||||
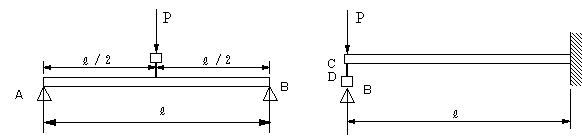 |
|||||
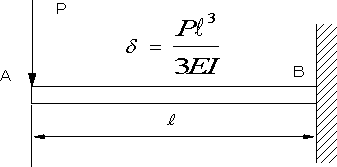 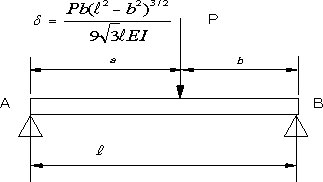 |
|||||
|
|||||
| 【解答例】 |
|||||
| 問題95 | 正方形断面を有する長さl=5mの木製単純支持はりにw=5000N/mの等分布荷重が作用する。このはりに生ずる最大曲げ応力をσmax=9.0MPaとして、はりに生ずる最大たわみを求めよ。ただし木材の縦弾性係数をE=11.0GPaとする
。 |
||||
| 【解答例】 |
|||||
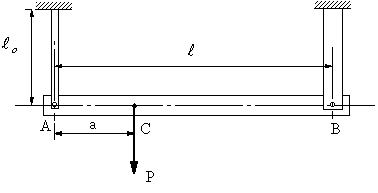
| 問題96 | 剛性板が材質や横断面積の異なる2本の細い棒で支えられている。これらの棒の延びが等しくなるようにするには左端からどの位置に荷重Pを作用させればよいか。まだ左右の棒に働く引っ張り力P1、P2はいくらか。ただし、棒と剛性板はピン結合されているとし、また左右の棒の断面積、ヤング率はそれぞれA1、A2、E1、E2とする。 |
||||
 |
|||||
| 【解答例】 |
|||||
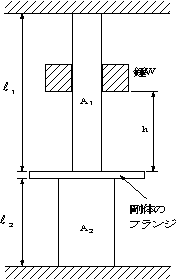
| 問題97 | 図のように、重さW[N]の錘を高さhから落下させ、フランジに衝突し、一体となって変位するとき、フランジの垂直方向の変位の最大値δmaxとする。錘を静的に錘をフランジに載せたときの変位δoとして、δmaxを求める。棒1と棒2はそれぞれ断面積をA1、A2とし、縦弾性係数は両材ともEである。 |
||||
 |
|||||
| 【解答例】 |
|||||
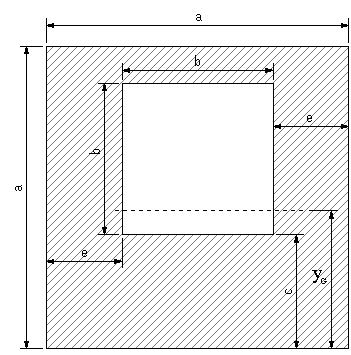
| 問題98 | a=80mmの正方形断面に、下面からc=30mmの位置に、b=40mmの正方形の穴が開いている。この断面の中立軸の位置を求め、断面二次モーメントを計算する。e=20mm | ||||
 |
|||||
| 【解答例】 |
|||||
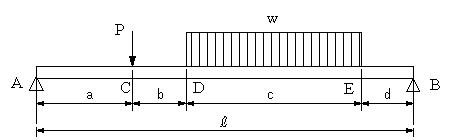
| 問題99 | 図の梁の場合に、せん断力、曲げモーメント、せん断力図、曲げモーメント図、曲げモーメントの最大値と生ずる位置を求める。ただし、AC=a=2m,
CD=b=1m,DE=c=4m,EB=d=1m,AB=L=8m,P=2kN,w=2kN/m |
||||
 |
|||||
| 【解答例】 |
|||||
| 問題100 | 図1の三角形の図心、図1,図2の断面二次モーメント、断面係数を計算する。 |
||||
|
|||||
【解答例】 |
「はじめての材料力学」サポートページ >材料力学の典型的な問題 PartⅡ