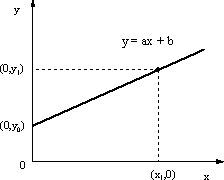| �͂��߂� | |||||||||||||||||||||
| �@ �@�����ł�1�̗ʂ��������ω������A����ɂ���Č��܂�ʂ𑪒肵�ē������ʂ���2�̗ʂ̊Ԃ̊W�ׁA���҂̊Ԃ̊W����ڗđR�ɂ���ɂ̓O���t�Ƀv���b�g���Ċw�I�ɕ\�����邱�Ƃł���B���̌�A���̃O���t�̌`��A����ɁA�Бΐ��◼�ΐ��Ƀv���b�g�����肵�Đ�����\�z���A�����ɂ��A���҂̊W���ʓI�ɕ\�����ƂɂȂ�B�������邱�Ƃɂ����2�̗ʂ̊W�����m�ɂȂ�B �@�ŋ߂́A�\�v�Z�\�t�g���g���A�p�\�R����ŃO���t�����쐻���邱�Ƃ��قƂ�ǂŁA�菑���̃O���t�ȂǍ쐬���Ȃ����A�O���t���쐬�����{�I�Ȓm���͕K�v�ł���Ɗ����Ă���B �@�p�\�R�����܂����y���Ă��Ȃ����C�w��������v���H�w�̃m�[�g���甲���������̂��Љ��B �@ |
|||||||||||||||||||||
| 2.1 | �O���t�ɕ\�����@ | ||||||||||||||||||||
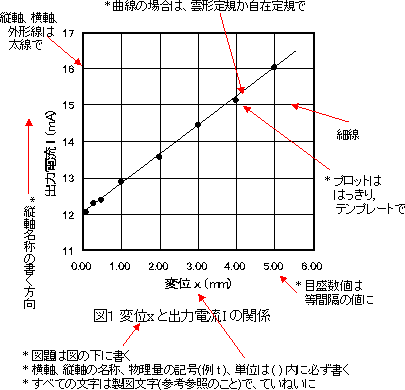
| �@ �@ 2�̗ʂ𗼎��Ɏ��A����l��\���_����ᎆ�Ƀv���b�g����B�����Ă����̓_�̊W���ł��悭�K�����钼����Ȑ��������B �@�c���Ɖ����̖ڐ���̎����ł��邪�A���z�I�ɂ́A����l�̗L�������̍Ō�̌��̂P�����ᎆ��1�ڂɂȂ�悤�ɑI�Ԃׂ��ł���B���������ۂ̏ꍇ�͕s�\�ȏꍇ���������A�L�������S����\���ł���悤�ɐS������ׂ��ł���B �@����l��\���}�[�N�͏������ƌ��ɂ����̂ŁA����~�̃}�[�N���傫���́A1.5mm�`2mm���x���K�Ƃ���Ă���B����ȉ��ɂ���ƁA�_�����G���ȂǂɈ�������Ƃ��A�k�������̂����ʂł���̂Ō��ɂ����Ȃ��Ă��܂��B�w��ȂǂŔ��\����Ă���_���̐}�ʂ����K���Ċw�K���������悢�B |
|||||||||||||||||||||
| �@ | |||||||||||||||||||||
| �� | �O���t��`���Ƃ��̒��ӓ_ | ||||||||||||||||||||
|
|||||||||||||||||||||
| �@ | |||||||||||||||||||||
| �� | �ΐ��ڐ��ɂ��� | ||||||||||||||||||||
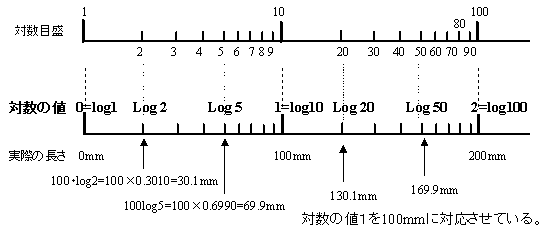
| �@�ΐ��̒l�́Alog1=0�Alog2=0.3010�Alog3=0.4771�Alog5=0.6990�Alog10=1�Alog100=log102 =2log10=2�Alog1000=log103=3�ł���̂ŁA�ΐ��ڐ��Ǝ��ۂ̒����͐}�̂悤�ɂȂ��Ă���B�]���āA�ΐ��ڐ��̐��l�̂Ƃ���ɓ_�����A��p�ΐ��̒l�ɂȂ��Ă���B �@���̐}�ł́A�ΐ��@log 10 = 1��100mm�ɑΉ������ĕ\���Ă���B �@ |
|||||||||||||||||||||
 �@�@ |
|||||||||||||||||||||
| �� | �@log5��A�_�̈ʒu�ɓ_�����Alog5=0.6990�ɂȂ�BB�_�́@log40 �ł���B�Бΐ��͏c���A�����̖ڐ�������ǂ��炩������ΐ��ڐ��ł���A�����Ƃ��ΐ����̏ꍇ�͗��ΐ��ƌ����Ă���B�@�v���b�g�������ʁA�_�������ɂȂ�A(6)���̎w���W�����藧���ƂɂȂ�B �@ |
||||||||||||||||||||
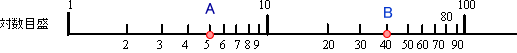 �@ |
|||||||||||||||||||||
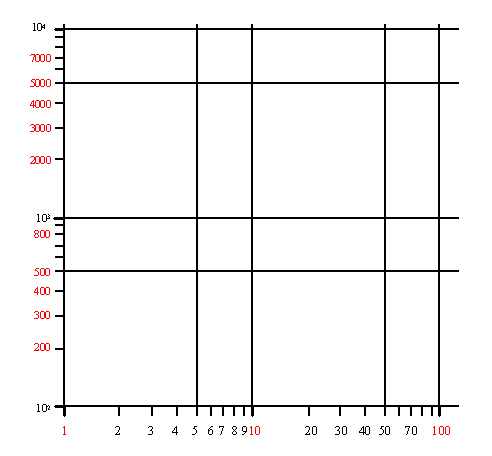 ���ΐ��p���ڐ���̗� |
|||||||||||||||||||||
| 2.2 | ���� y = ax + b�̏ꍇ | ||||||||||||||||||||
| �@ ���ᎆ�Ƀv���b�g���āA�_��D�����ς̋Ȑ��������Ȃ�A����lx , y �� �@ �@�@�@�@�@�@�@�@�@y = ax + b�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ (1) �̊W�ɂ���B�W���Aa, b �͒萔�ŁAb�͐}2��y���ƌ����_(0,y0)�� b�@= y0 �ł���B a�͒�����̂P�_�̍��W(x1,y1) ��ǂ݁A |
|||||||||||||||||||||
| ���瓾����B���������ꍇ�A�����Ȓ�K�Ő��̗����ɓ_�����ϓI�ɕ��z����悤�ɂ��Ă����A���������B �@ |
|||||||||||||||||||||
|
|||||||||||||||||||||
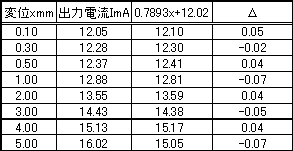
| �@ �@�\1�́A�ψʂ̑���ɗp����쓮�g�����X�̕ψ�x(mm)�ɑ���o�͓d��I(mA)�̊W�ŁA����l���v���b�g����ƒ���������ꂽ(�}3)�B �@ �@�@�@�@�@�@�@�@�@�@�@�@I = ax + b �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(3) �@ �Ƃ��āA�������(I,x)��2�_��^���āAa,b�@�̕����������A�W��a, b �����肷��B�}�R�̏ꍇ�A��}�����������2�_��ǂ݁A��(3)�ɑ�����Aa,b�Ɋւ�������������A����������āA a�Ab�̒l��B �@�@�@�@ |
|||||||||||||||||||||
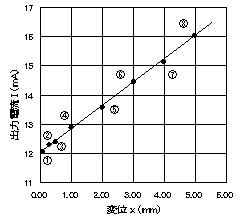 �@ �}3 �ψʌv�̏o�͓d��I�ƕψ�x�̊W �@ |
|||||||||||||||||||||
| �� | �����@�@����قǂ̐�������K�v�Ƃ��Ȃ��ꍇ | ||||||||||||||||||||
| �@ �@����l���W������̂ŁA�����4����2�Q�ɕ�����B�\1��x��I�̘a �@ |
|||||||||||||||||||||
| �@ �@���v�Z����B |
|||||||||||||||||||||
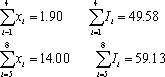 �@�@�@�@�@�@�@�@�@�@ �@ �@�@�@�@�@�@�@�@�@�@ �@ |
|||||||||||||||||||||
| ���ɁA2�Q�Ƃ̍������Ab����������B �@ �@�@�@y2 - y1 = a(x2-x1) �@�@�@���@a = ( y2 - y1)/(x2-x1)�@�@�@�@�@�@ (4) �@ |
|||||||||||||||||||||
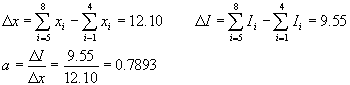 |
|||||||||||||||||||||
| �@ �@a = 0.785��������B����x�̑��a��a���|���āA�ς�I �̑��a��������A����8b�ɂȂ�B |
|||||||||||||||||||||
| b = 12.02��������B�]���āAI��x�̊W���� �@ �@�@�@�@�@�@�@�@�@I = 0.7896x + 12.02�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ (5) �@ ������B���ǁA�_�@�`�C��4�_�ƇD�`�G�̂S�Ă�̂��ꂼ�ꕽ�ϓ_��ʂ钼���̎������肵�����ƂɂȂ�B�ȒP�Ȋ��ɂ͐��x���ǂ��W�������肷�邱�Ƃ��ł���B |
|||||||||||||||||||||
| �@ | |||||||||||||||||||||
| 2.3 | �������Ƒo�Ȑ� | ||||||||||||||||||||
| �@ �@ �v���b�g�����_�� �@�@�@�@�@�@�@y = axn �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(6) �@�ŕ\�����Ƃ��A���ӂ̑ΐ������ �@�@�@�@�@ �@log y =log a + n log x �@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@(7) �@log y =Y, log a= A, log x=X�Ƃ����� �@�@�@�@�@�@�@Y = nX + A�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ (8) �ƂȂ�A�����ɂȂ�B2�̗ʂ̊Ԃ̊W���A��p�ΐ���������Ƃ������I�ȊW�ɂ���Ƃ��O�������Ă͂܂�B���ΐ��O���t�p���Ƀv���b�g����ƒ�����������B �@n�����Ȃ�A��ʂɕ������^�A���Ȃ�o�Ȑ��^�ƂȂ�B��(8)�ɁC�����@��x,y��ΐ��ɕς��Ă����ɏq�ׂ�ŏ����@��K�p�����n,A�����߂Ă���An,a��������B |
|||||||||||||||||||||
| �@ | |||||||||||||||||||||
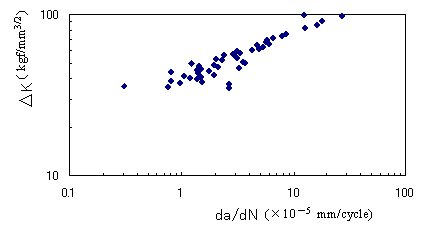
| �� | �y��1�z�@��J�����`�d���x�Ɖ��͊g��W���̊W |
||||||||||||||||||||
| ��K: ���͊g��W���@Stress intensity factor �Ђ��F���͐U���C�`�C���F�ޗ��萔 |
|||||||||||||||||||||
 |
|||||||||||||||||||||
| �}4 ��J�����`�d���x�Ɖ��͊g��W���̊W | |||||||||||||||||||||
| �� | �@ �@�y��2�z�@�J��Ԃ����́|�Ђ��݂̊W |
||||||||||||||||||||
��o : �ޗ��萔 �@�@�@�@�@�@�@�@��: �J��Ԃ��Ђ��ݍd���w�� Cyclic strain hardening factor |
|||||||||||||||||||||
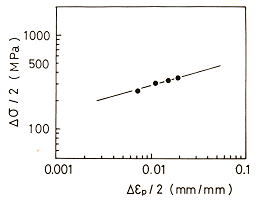 �}5 �J��Ԃ����́|�Ђ��݂̊W �@�@�@�@�@�@�@����0.212 �C�萔�Ђ���92.9 �CSS400 |
|||||||||||||||||||||
| �� | �w�����̏ꍇ | ||||||||||||||||||||
| �@���R���ۂɂ͎��̎��ŕ\�������̂������B �@�@�@�@�@ ���̏ꍇ�����ӂ̑ΐ����Ƃ� �@�@�@�@�@ ���̂悤�ɒu��������B �@�@�@�@�@ y��ΐ��ɁA�Бΐ��O���t�p���Ƀv���b�g����ƒ����ɂȂ�B �@�@�@�@�@ |
|||||||||||||||||||||
| �@���̊��̏ꍇ�Ɠ��l�ɁAA,B�����肷��B���ɏq�ׂ�ŏ����@�ŋ��߂Ă��ǂ��B | |||||||||||||||||||||
| �@ | |||||||||||||||||||||
| 2.4 | �ŏ����@�ɂ��2�̗ʂ̊W�������߂���@�ɂ��� |
||||||||||||||||||||
| �O�f�̏o�͓d��I�ƕψ�x�̃f�[�^�̊W�� �@�@�@�@�@�@�@�@�@�@I = ax + b�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ (9) �̈ꎟ���ŕ\�����Ƃ��An�̕ψʁAx1,x2, ----, xn �ɑ��ēd��I�̑���l���AI1, I2, ----, In �ł������Ƃ��ɁA�œK�Ȓ萔�Aa, b �����肷�邽�߂ɍŏ����@��K�p����B �@��(9)�ɂ��ꂼ��̃f�[�^��������B |
|||||||||||||||||||||
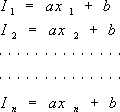 �@�@�@�@�@�@�@(10) �@�@�@�@�@�@�@(10) |
|||||||||||||||||||||
| �@��(10)���ϑ��������Ƃ����B ��(10)�͖��m����a, b�Q�ŁA��������n�ł���̂Ŗ�������a, b�͑��݂��Ȃ��B�ψ�xI�ɂ����ۂ͌덷���͂��邪�A�����ł͌덷���Ȃ����̂Ƃ��āA�d��I1, I2, ----, In �� �덷���A���ꂼ��Az1, z2, ----, zn �Ƃ���� �@ |
|||||||||||||||||||||
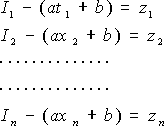 �@�@�@�@�@�@�@�@�@�@�@�@�@(11) �@�@�@�@�@�@�@�@�@�@�@�@�@(11) |
|||||||||||||||||||||
| ��������B a, b �̒l�͖��m�ł���̂ŁA a, b��ϐ��Ƃ��āA�덷�̓��̘aS |
|||||||||||||||||||||
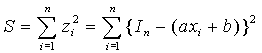 �@�@�@�@�@�@�@(12) �@�@�@�@�@�@�@(12) |
|||||||||||||||||||||
| �@ ���ŏ��ɂȂ�悤�Ɍ��肷��̂��ŏ����@�̍l�����ł���BS���ŏ��̎��AS��a��b�Ŕ��������l��0�ł���̂Ŏ��������藧�� �@ |
|||||||||||||||||||||
| ��(12)��a��b�Ŕ�������� |
|||||||||||||||||||||
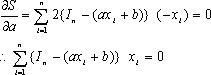 �@�@�@�@ (14) �@�@�@�@ (14) |
|||||||||||||||||||||
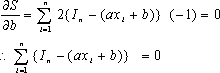 �@�@�@(15) �@�@�@(15) |
|||||||||||||||||||||
| �X�Ɏ�(15)�ό`����ƁA | |||||||||||||||||||||
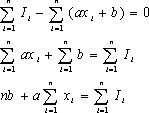 �@�@�@�@�@�@ �@(16) �@�@�@�@�@�@ �@(16) |
|||||||||||||||||||||
| �ƂȂ�B �X�Ɏ�(16)�ό`����ƁA |
|||||||||||||||||||||
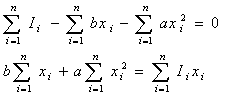 (17) (17) |
|||||||||||||||||||||
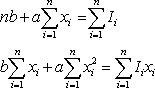 �@�@�@�@�@�@�@(18) �@�@�@�@�@�@�@(18) |
|||||||||||||||||||||
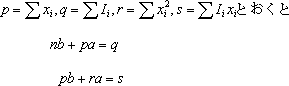 (19)(20) (19)(20) |
|||||||||||||||||||||
| ��(19)�Ǝ�(20)��a, b �Ɋւ���A���������ł��邩�炱��������� |
|||||||||||||||||||||
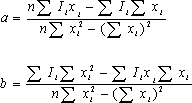 �@�@�@�@�@�@�@�@(21) �@�@�@�@�@�@�@�@(21) |
|||||||||||||||||||||
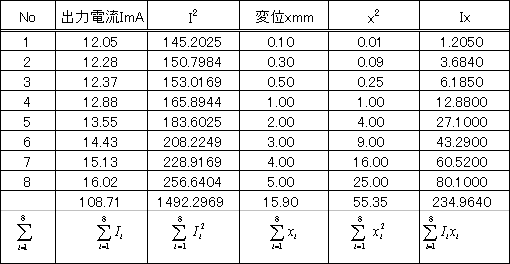
| ��������B ��(21)�̉E�ӂ̒l��Excel�ŋ��߁A�������� |
|||||||||||||||||||||
 |
|||||||||||||||||||||
| �@*��̕\��I2�̍��ڂ͕K�v����܂���B�ŐV��Excel�͎g�p�������Ƃ�����܂��A��L�\�̒l���v�Z���āA���̐����ɑ����������VBA���g�����ȒP�ŗǂ��Ǝv���܂��B �@Excel�̌v�Z�ɕs����ȕ������������Q�l�ɂ��ĉ������BVBA�ɂ��ŏ����@�̃}�N������������������Q�l�ɂ��Ă��������B �@ |
|||||||||||||||||||||
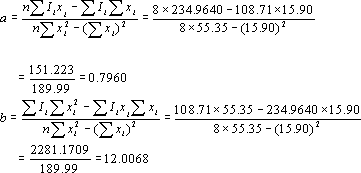 |
|||||||||||||||||||||
| �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@a = 0.7960, b = 12.01 ��������B �@���݂�Excel���g����a, b �̌v�Z�͊ȒP�ɂł���B����ɁCVBA�ɂ��}�N���������s���C�}�E�X�E�����N���b�N�Ōv�Z���\�ɂȂ�B �@ |
|||||||||||||||||||||
| �� | �Y���Ђ��ݕ����Â��Ǝ����m���̊W |
||||||||||||||||||||
| �@�Y���ό`������悤�ȌJ��Ԃ��̂Ђ��ݕ�������(�Ђ��ݐU����2�{)�Ɣj�f�����m���̊Ԃɂ͎��������藧���Ƃ��m���Ă���B �@�@�@�@�@�@�@�@�������E�m�������b�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ (22) �@�@�@�@�@ ��J�����̌��ʁA�\3�Ɏ����f�[�^������ꂽ�B |
|||||||||||||||||||||
�\3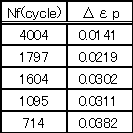 |
|||||||||||||||||||||
| ��(22)�̗��ӂ̑ΐ������ƁA | |||||||||||||||||||||
| �@ �@ |
|||||||||||||||||||||
| �@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@E = - ��N + b �ƂȂ�A�����̎��ƂȂ�B�����ŁA����C�����肷�邽�߂ɍŏ����@��K�p����B |
|||||||||||||||||||||
�\4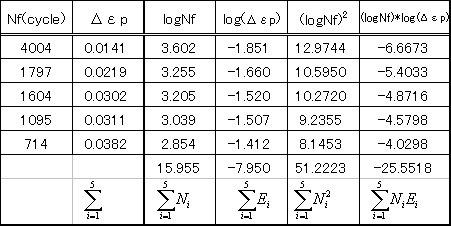 |
|||||||||||||||||||||
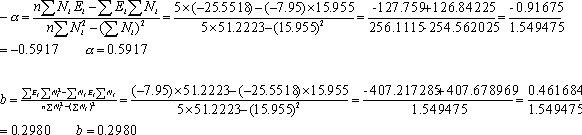 |
|||||||||||||||||||||
| ���L�������͍l�����Ă��Ȃ��B |
|||||||||||||||||||||
logC=b �ł��邩�� C = 100.298 =1.986 �ƂȂ�A�W���� �@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�������E�m��0.5917���@1.986�@ �ƂȂ�B �@ |
|||||||||||||||||||||
| �� | ���͐U����a�Ɣj�f�J�Ԃ���Nf�̊W�@S-N�Ȑ��@---�@�Бΐ��O���t�p���Œ����ɂȂ�� |
||||||||||||||||||||
| �@S-N�Ȑ��̌`��͎�X�̎�����Ă���Ă���B�}6�́A�Бΐ��O���t�p���Ƀv���b�g�����ꍇ�ł��邪�A�����ƂȂ邱�Ƃ���A | |||||||||||||||||||||
| �@�@ |
|||||||||||||||||||||
| �@�ŕ\�����B | |||||||||||||||||||||
| �@�@�@�@ |
|||||||||||||||||||||
| ����x,y�̎��ɍŏ����@��K�p����B | |||||||||||||||||||||
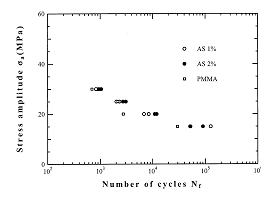 �}6�@AS,PMMA(����)�Ƃ̕����ނ̂r�|�m�Ȑ� |
|||||||||||||||||||||
| *�}6�͈ȑO�֗��ȃ\�t�g������A�ڐ�����w���ŏ������ނ��Ƃ��o�������AExcel�ł͕s�\�ł������̂ŁA�O���t�ɂ͖ڐ���̕��������Ȃ���PowerPoint �ɐ}�Ƃ��ăR�s�[���A�p���[�|�C���g�̕����Ŗڐ������͂��Ă���B�C���X�g���[�^�[�ł͉\�ł���B |