| ◆作用線が一致しない平行力の合成平行力の合成 | ||||
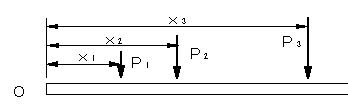
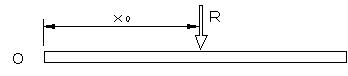
| 図7のように2つ以上の平行な力が作用する場合の合力を求める。1点に作用する多くの力と同様に、力の効果が同じであればよい。平行力の場合は、作用点が異なるから、回転する作用が生ずるので,モーメントも考慮する必要がある。O点に関するモーメントを考えるとき、運動の効果が等しい(この場合は、平行移動させる効果、回転させる効果) P1 +P2 +P3 = R (7) (図7(a)のモーメントの和Mo)=(図7(b)のモーメント、−Rxo ) (8) となる必要がある。従って,Mo=−Rxo となる。 |
||||
|
||||
| 図7 P1 ,P2 ,P3の平行力の合成,合力の大きさRと作用する位置xo | ||||
| 合力Rと作用点の位置xoを上式の値にとれば,(a)の場合と全く同じ回転の効果と平行移動の効果となる。多くの力を取り扱うよりも,1つの力で代表させることができれば計算も単純化され,解析も簡単になるので,必要に応じて,合成したり,分解したりする。 | ||||
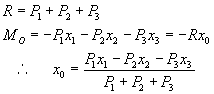 (9) (9) |
||||
| 【例題4】平行力の合成の応用 ---重心の位置を求める場合 | ||||
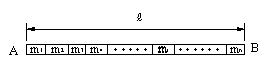
| 水平に置かれた棒をn個の部分に分割する。 分割された物体の各部分に作用し、分布している重力は、方向が同じ(鉛直下向き)で、平行である。この力を合成し、1つの合力にまとめたとき、この合力の作用線の位置が重心である。 合力の大きさWは、前述の結果から,物体の質量Mとおくと |
||||
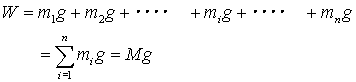 (10) (10) |
||||
| Aに関するモーメントT’は、図8(a)と図8(c)の場合に等しくなることが必要(合力の説明の項参照)があるのでモーメントを求める。 | ||||
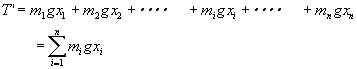 (11) (11) |
||||
|
||||
 (c) 重力を合成 |
||||
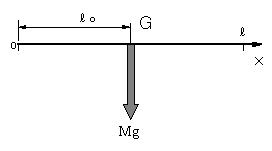
| 図8 合力の作用する位置が重心G | ||||
| 簡単にするために,n等分の時、 | ||||
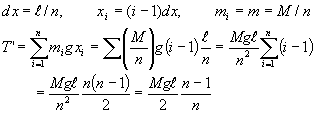 (12) (12) |
||||
| 極限値を求めると重力によるモーメントの総和T’は | ||||
| |
||||
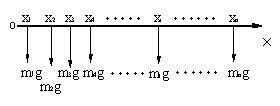
| となる。 同じ重力によるモーメントの総和T’を求めるのに,積分法を利用して求めてみる。 微小部分dxに作用する重力は,単位長さ当たり(M/l)gであるから、dxの部分には,(M/l)gdxの重力が作用する。A点からの距離x、この部分のモーメントΔTは、 ΔT = (M/l)gdx・x (区分積分法のAi) |
||||
| |
||||
| 上式を0からlまで積分を行う(区分積分法,Aiの和をとり、極限値を計算に相当)と | ||||
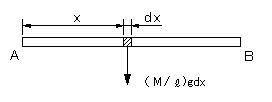 図9 |
||||
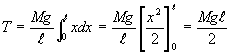 (15) (15) |
||||
| なる。一方、W(=Mg)によるモーメントMAは、作用点l0 と置き MA = W・l0 (16) 力を合成しない時のモーメントの大きさと合成した力によるモーメントの大きさは等しい,T=MAから、 |
||||
| となる。作用点l0 が重心の位置で、断面が一様な棒の場合は中点である。 |