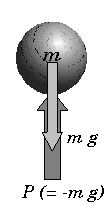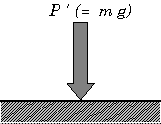| 材料力学ばかりでなく、工学一般で、当たり前のように扱われている力学の基礎的知識について解説する。公式を覚えていただくことは目的ではなく、すでに学んだ簡単な事項について、どういうことを意味しているのか、じっくり考えて理解していただくことが目的である。そうすることによって、工学の専門科目にごくすんなりと入れることを期待している。 |
||||||||
| ● 力とモーメント | ||||||||
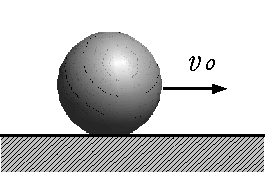
| 重量物を持ち上げる、ボウルを投げる、コンクリートの壁を強く押してみる、棒を両手でもって曲げてみるなど私たちが力を感じるときである。この力を物体に与えると物体はどのような状態変化を生ずるかを調べると力の性質などが理解できそうである。 ■ 力と運動 ------ ニュートンの運動の3法則 ニュートンは力と物体の運動の経験的事実から、3つの法則にまとめた。力学の基礎であることは勿論、運動を扱わない材料力学においても力の性質や釣り合いなどの諸現象を理解する上で極めて重要である。 ◆運動の第1法則(慣性の法則) 「物体に外部から力が作用しなければ、静止している物体は静止の状態を続け、運動 をしている物体は等速直線運動を続ける」 |
||||||||
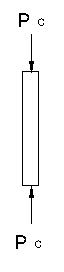
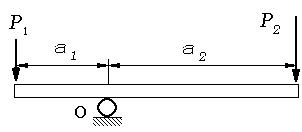
図1 |
||||||||
| 【解説】 等速直線運動の速度が0の特別な場合が静止であること、また、多くの力が物体に作用しても、それらの合力が0(釣り合いの状態)であれば、力が働かない状態と同じであることに注意すべきである。材料力学では「力が作用しなければあるいは釣り合っていれば、物体は静止する」と考えて良い。 |
||||||||
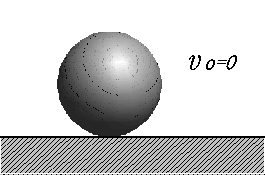
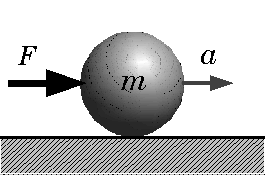
◆運動の第2法則 「質量mの物体に外部から力Fが作用すると、物体は力と同じ方向に、力の大きさに比例し、物体の質量に反比例する加速度aを生ずる」 F=ma (1) 運動の状態を定量的に示したもので、第1法則のF=0の時、加速度a=0(速度は変化しない)では時間に関係なく,常に一定の速度Voで運動を続けることを示している。このうち,Vo=0の特別な場合が静止である。 |
||||||||
 |
||||||||
| 図2 質量mの物体に外部から力Fが作用 | ||||||||
運動の状態を定量的に示したもので、第1法則のF=0の時、加速度a=0(速度は変化しない)では時間に関係なく,常に一定の速度Voで運動を続けることを示している。このうち,Vo=0の特別な場合が静止である。 |
||||||||
◆運動の第3法則 (作用・反作用の法則) 「物体Bが他の物体Aにある力を作用させると,AはBから必ず大きさが等しく向きが反対の力の作用を受ける」 |
||||||||
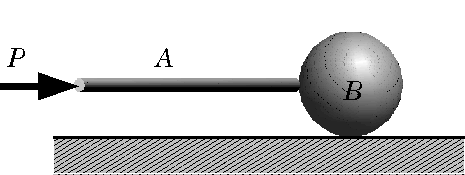 (a)物体Aを介して物体BにPの力が作用 |
||||||||
 (b)物体Aは物体BからP’の力を受ける P : 物体Bに作用した力 P’: 物体Bから受けた反作用力 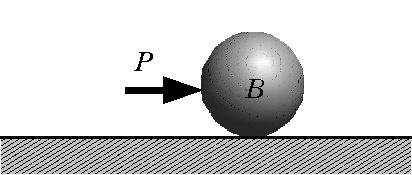 (c)物体BにはPの力が作用 |
||||||||
| 図3 P : 物体Bに作用した力 , P’: 物体Bから受けた反作用力 |
||||||||
| P=P’であり、向きは反対。AとBに作用する力の大きさは同じで無関係ではないこと、力はこの法則により伝達されることがわかる。 | ||||||||
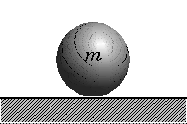
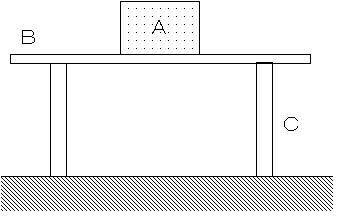
| 【例題1】台の上に置かれた質量mの物体の場合 | ||||||||
|
||||||||
| 図4 質量mの物体に作用する反作用力P 下向きを+にとっている | ||||||||
| 台の上に置かれた質量mの物体は静止している。これは物体に作用する力が釣り合っている。地球上の物体には重力が作用する。質量mの物体にはmgの重力が作用している。この重力が台をmgの力で押して作用している。作用反作用の法則から,物体は,向きが反対(上向き)で大きさが等しい力(P=−mg)を台から受ける.この反作用の力と重力が釣り合って(P+mg=0),物体は静止する。 |
||||||||
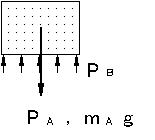
| 【例題2】構造部材に作用する力の解析 | ||||||||
| 机の上に置かれた、質量mAの物体について考える。作用・反作用の関係は物体Aと机の天板Bの接触面で生ずる。 PA=−PB (2) |
||||||||
|
||||||||
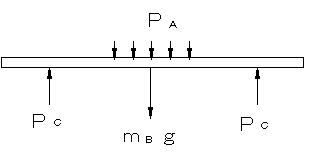
| 重力加速度gとすると物体には、重力mAgの重力が作用する。物体Aに作用する力は、PA(重力mAg)とPB(天板からの反作用)である。物体Aは、静止しているのであり、これらの2つの力は釣り合っている。 PA + PB =0 ∴PA =− PB (3) となり、向きは反対で,大きさは等しい(いずれもmAgである)。 次に,天板Bに作用する力は、PAと天板の重力mBgと机の4本の脚Cからの反力4PCであり、釣り合っているから、 PA +mBg+4PC =0 (4) 脚Cは、床からと天板BからPC の力を受けて釣り合っている。このように、部材間には、作用・反作用の法則によって力が働き、部材を通して力が伝達され,その大きさは、互いに無関係ではないことが解る。このことように、多数の部材からなる構造物などの部材に働く力を解析することができる。 材料力学では「力が作用しなければ、物体は静止する」と考えて良い。また、多くの力が物体に作用しても、それらの合力が0(釣り合いの状態)であれば、力が働かない状態と同じである。 |