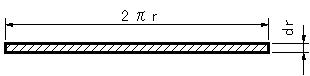
| 2�@�����@ | ||||
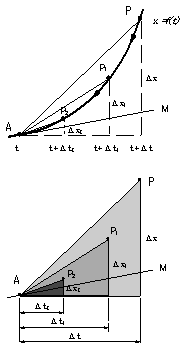
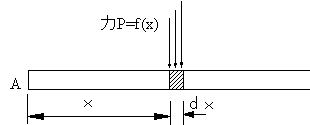
�@�����@���Ȋw�ɂ����錻�ۂ����������@�Ƃ��ĕK�{�̕��@�ł���B���C�����w�܂ōs�����Ƃ��l����B������s km�Ƃ���B�r���C�ŏ��͂����������āC����Ƃ��납�玞�Ԃ��Ȃ��̂ő������Ƃ���B���v���Ԃ͂����ł������B�����w�܂ł̕��ϑ��x�́Cs/t [km/��]�ƂȂ邪�C�����Ă����Ƃ��̑��x�C�����Ă����Ƃ��̑��x�͂͂����肵�Ȃ��B�����ŁA���鎞���ɂ�����u�ԓI�ȑ��x�����߂悤�Ƃ���̂������̍l�����ŁC���̂��Ƃ����ɏq�ׂ�B �@�����^�������Ă��镨�̂�����C�^�����J�n��C����t�ƈʒu�����v�����C�ʒu�Ǝ��Ԃ̊W���Cx=f(t)�̊W������ꂽ�B�����Ɏ��Ԃ��C�c���Ɉʒu�����Ƃ�Ɛ} �S�̂悤�ɃO���t�ŕ\����Ƃ���B�O���t��ɁC�`�i���C���j�_�C���������烢�����Ԍ�̈ʒu�o�it+����,x+��x�j�_���Ƃ�B���̎��C�`�̈ʒu���狗����x�����i���ƂɂȂ�B�`�o�Ԃ̕��ϑ��x�u�� |
||||
| �@�@�@�@�@�@�@�@�@�@�@�@�@�@ |
||||
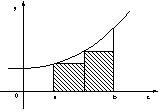
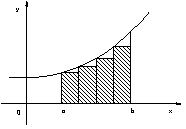
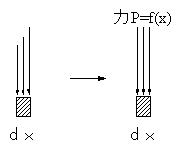
| �ł���B�����̊Ԋu���X�ɏ��������C�o�P �� �o�Q �̂悤�ɂƂ��ĕ��ϑ��x�����߂Ă݂�B�O���t��ł́C�o�_�� �`�_�ɋ߂Â��Ă䂭�B���̎��C�Ɍ��̍l������K�p���āC���� ���O�Ƃ��Ă݂�B�@�@ | ||||
| �@�@�@�@�@�@�@�@�@�@�@�@�@ |
||||
| �u�́C�u�Ԃ̑��x�ł���C���̒l�x�ƒ�`����B | ||||
|
||||
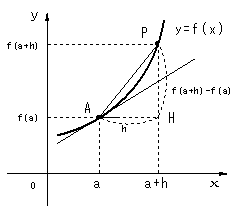
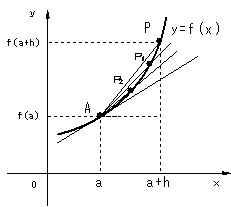
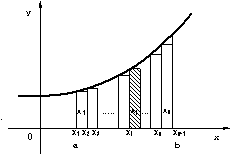
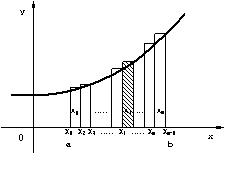
| �@�}�S(b)���� �����`�o�̌X���́C���� ���O�̋Ɍ����l����Ƃ`�_�ɂ�����Ȑ��̐ڐ��`�l�ɋ߂Â����Ƃ������ł���B �@���ɁC��ʂ̊�y=F(x)�ŁC���̋Ɍ��l�����߂Ă݂�B �@�}5�ŁA���̎��Œ�`�����l�����������炁�{���ς��Ƃ���f(x)�̕��ϕω����ƌ����D���Ԃ��A����x=f(t)�ɂ�����A���Ԃ����炔�{�����̊Ԃ̕��ϑ��x�ɑ�������D |
||||
| �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ |
||||
|
||||
�@f(x)�̕��ϕω����ɂ����āA��������Ȃ��O�ɋ߂Â��Ƃ��A���̋Ɍ��l����y=f(x)��x=a�ɂ���������W���C�܂��͕ω����ƌ����Af'(a)�ŕ\���B |
||||
| �@�@�@�@�@�@�@�@�@�@�@�@�@ |
||||
| �@�����W��f'(a)�́C�}�ɂ����āA�o�_������Ȃ��`�_�ɋ߂Â���Ɓih���O�j�A�`�o�́A�`�_�ɂ�����y=f(x)�̐ڐ��ɋ߂Â��l�q��������B�]���āA�Ɍ��l��f'(a)�́A�`�_�ɂ�����y=f(x)�̐ڐ��̌X���ƂȂ�B | ||||
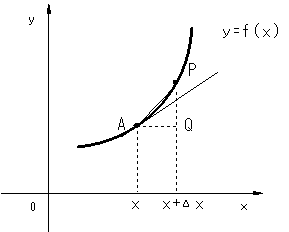 |
||||
| �} �U | ||||
| �������C���������ƒu�������āA �@�@�@�@�@�@�@�@�@�@ |
||||
�@f'(x)����f(x)�̓����Ƃ����BX�̊�f(x)����Af'(x)�����߂邱�Ƃ��A �@�@�@�@�@�@�@�@�@�@�@�u��f(x)�����ɂ��Ĕ��������v �ƌ����B �@y=f(x)=x2�̏ꍇ�̌v�Z�����Ă݂�B |
||||
�@�@�@�@�@�@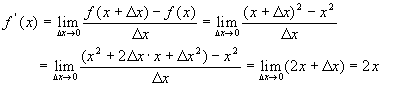 �@�@(10) �@�@(10) |
||||
| �@f(x)=x3,x4������, xn�̏ꍇ�̌v�Z�����Ă݂�ƁA���̖@��������D |
||||
| �@�@�@�@�@�@�@ |
||||
�@�]���āA���������Ɍ��l���v�Z����K�v�������Ȃ�B���̊��ɂ��Ă��A���łɌv�Z����Ă���A�悭�g�����́i�Ⴆ�A�O�p���A�w�����Ȃǁj�������o���A���G�ȏꍇ�́A�ϕ��Ɠ��l�A���w�����W�����p����悢�B �@�@ |
||||
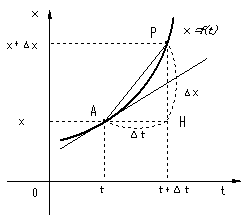
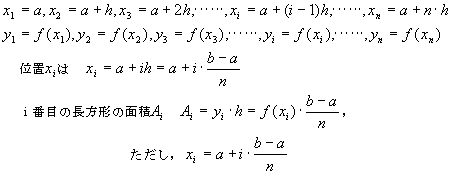 (12)
(12)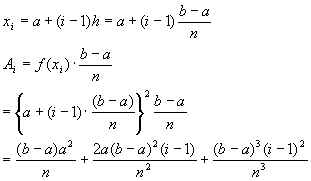 �@�@�@�@�@(13)
�@�@�@�@�@(13)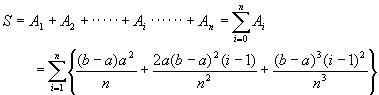 �@�@(14)
�@�@(14)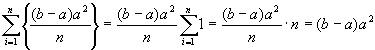
 �@�@�@
�@�@�@ �@(16)
�@(16) �@�@�@�@�@�@�@�@�@�@�@�@�@�@(17)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@(17)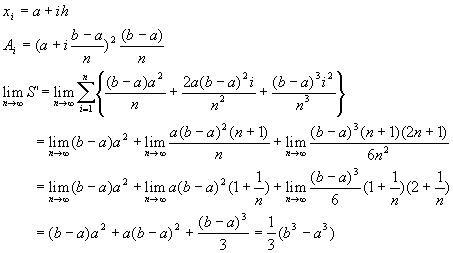 �@�@�@(20)
�@�@�@(20)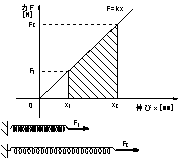
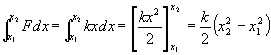 �@�@�@�@�@�@�@�@(26)
�@�@�@�@�@�@�@�@(26)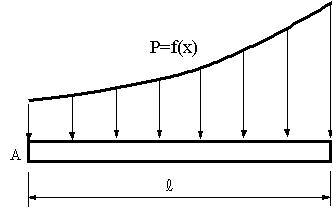 �@�@�@�@
�@�@�@�@ �@�@�@�@
�@�@�@�@
 �@�@�@�@�@�@�@�@�@�@(31)
�@�@�@�@�@�@�@�@�@�@(31)
 �@�@�@�@�@�@�@(32)
�@�@�@�@�@�@�@(32) �@�@�@
�@�@�@