| 高校で学んだ数学や物理、化学などの知識は、本来、生活する上で必要な事項であるが、将来、生活を便利にする機械やものなどを作り、そして、これらを人々に提供するプロフェッショナルとして活躍する技術者にとっては、物理や化学などの自然科学は,最も基本をなす知識を与えてくれるものである。 自然科学においては,自然界の法則が導かれた過程と法則を理解し,この法則を述べる専門用語をきちっと理解することは重要である。その際、数量間の関係を求めるときの手段として,数学は必須の知識である。高校まで、物理、化学や数学は別々の科目として扱われてきたので、学生諸君は、それらは互いに、関係のない科目と感じている方が多い。しかしながら、工学は、自然科学における法則の応用であり,物理、化学や数学は、密接に関係するものであり、特に、数学は、自然科学科目の共通言語のようなものであることを工学を志す学生諸君は自覚していただきたい。 材料力学では,力の釣り合い,モーメントの釣り合いなどの力学的知識を使い,材料中に生ずる抵抗力を計算によって導き,設計計算に必要な基本的な法則を定量的に明らかにする。この時,物理における力学と量的な関係を導く数学の知識が必要とされる。 ここでは,数学と力学の基礎的事項について述べる。公式を覚えていただくことは目的ではなく、すでに学んだ簡単な事項について、どういうことを意味しているのか、じっくり考えて理解していただくことが目的である。そうすることによって、工学の専門科目にごくすんなりと入れることを期待している。 |
||||||||
| 1 関数の極限値 | ||||||||
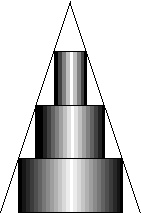
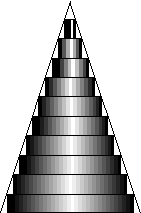
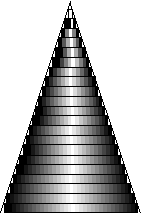
関数の極限値は、微分、積分の基礎であるとともに、工学においては、現象の結果が,十分時間的が経過した後どうなるか、あるいは,遠く離れた位置における値など考察するときに重要である。 図 1(d)の円錐の体積を考えてみる。円錐の体積を簡単に求めるために,(a)のように同じ高さhの円柱を階段状に積み重ねてみる.三角形は円錐の外形線であるが,これに収まるように同じ高さの円柱を重ねる。円柱の高さが小さくなると(図 1(b),(c))円柱の外形線との隙間の面積は小さくなり,円柱の体積の合計は円錐の体積に近づくことが予想される。高さhを0にしたら,円柱は存在しなくなるが,高さhを限りなく0に近づける状態を想定することが極限で,この状態をh→0と表現する。h→0の極限では,階段状の部分は直線に近づき,ほぼ,階段状の円柱を重ねた体積の合計は,円錐の体積と同じくなることが考えられる。 |
||||||||
|
||||||||
| 図 1 積み重ねる円柱の高さを小さくしてゆくと円錐の体積に近づく | ||||||||
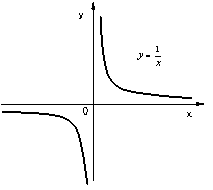
簡単な極限値の例を見てみる。図 2はy=1/xのグラフである。グラフの形からわかるように,xが限りなく大きくなり,∞大になったとき,yの値は限りなく0に近づく。このことを極限値の表現で |
||||||||
|
||||||||
| |
||||||||
| 次の例は工学でよく使われる極限値の式である。 別の表現では と書く。xが非常に小さいとき、sinxとxは近似的に等しい。 |
||||||||
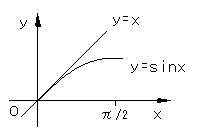
| 材料力学においても、せん断ひずみ、圧力容器に生ずる2軸応力を導く式で、近似式として、前式の結果から、次のように考える。xが小さいとき、三角関数sinxは、近似的にxに等しい。式が簡単になり、微分,積分がしやすく、計算もしやすくなるからである。 また、図式的には、xが小さくなると、y=sinxのグラフは、y=xのグラフに近づくことを意味している。 (sinx)'=cosxであり、x=0とき,cos0=1で、sinxのx=0の接線の傾きは、1となって、y=x の傾きと一致している。つまり、 y=sinxのx=0における接線はy=xである。 |
||||||||
 |
||||||||
| 図 3 xが小さくなると y = sinx と y = x のグラフは、ほぼ一致する | ||||||||
同様に, の近似式もよく使われる。近似式を使うことにより、数式の扱いが簡単になることから多用されている。つまり、一例として、tanxの積分より,xの積分の方が簡単だからである。 |