(a)
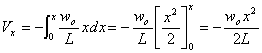
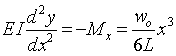
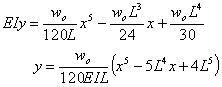
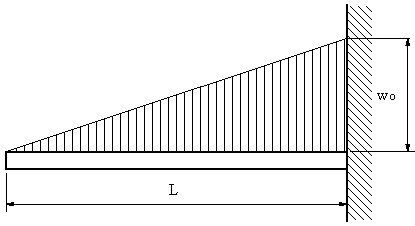
図1
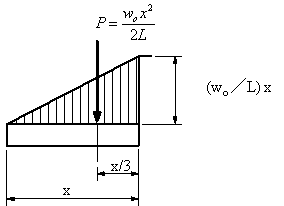
図2
上の方法ではxのはりの部分に作用する合力の大きさとこの合力の作用位置から曲げモーメントを求めた、積分する方法でも求めることが出来る。

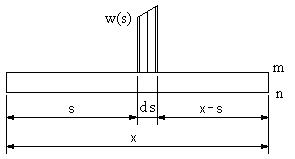
図3
| 【問題11】 (a) |
|
| 【解】 | 図1の場合 せん断力Vxと曲げモーメントMx、たわみyを求める。 |
| 図2のように、座標軸を取ると分布荷重の式は | |
| |
|
| で与えられる。せん断力Vxは、 xの長さのはりの部分に作用する分布荷重の合力Pとなり、図2の三角形の面積に相当し、作用点は図心x/3である。 | |
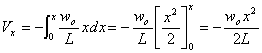 |
|
| xの位置の断面に生ずる曲げモーメントMxは | |
| |
|
| となる。 | |
| たわみの式から | |
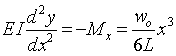 |
|
| となる。両辺を積分して | |
| |
|
| さらに、両辺を積分して | |
| |
|
| となる。境界条件は x=Lでたわみ角θ=0, たわみy=0である。 | |
| x=Lでたわみ角θ=0から | |
| |
|
| x=Lで たわみy=0から | |
| |
|
| 従って、たわみの式は次のようになる。 | |
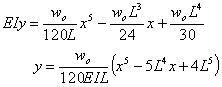 |
|
 図1 |
|
 図2 |
|
| * | 積分法でMxを求める方法 上の方法ではxのはりの部分に作用する合力の大きさとこの合力の作用位置から曲げモーメントを求めた、積分する方法でも求めることが出来る。 |
 |
|
 図3 |