| 多くのテキストでは、応力は,材料の単位面積当りに作用する荷重の大きさがσであることを表すと同時に荷重Pが作用したときに、内力の大きさが単位面積当りσであると述べられている。「はじめての材料力学」では解説しているが、「内力とは何か」を詳細に述べると原子論的記述が必要になってくる。ここでは、応力を理解していただくために再度、取り上げて解説する。「材料の強度と破壊」の学問につながる意味でも重要であると考えている。 |
|
| ■ | 2つの原子の間に作用する力とポテンシャルエネルギー -------- 原子論的考察 |
| 2つの原子の間に作用する力とポテンシャルエネルギー(位置によって変化するエネルギー)は,次のようになる。原子が引き合う力,引力は各電子は他方の陽子から引力を受けるにより生ずる。これに反し,反発する力,斥力(反力)は次の(1), (2)によって生ずる。 (1) 2個の電子の反発 (2) 原子核の陽子の総合反発 |
|
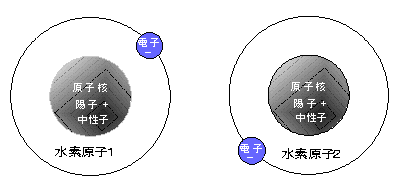 水素原子の場合 |
|
| 図1は横軸に原子間距離r,引力(-)として,斥力を(+)として,縦軸を通常とは反対にとり合力を求めた結果であるが,図1に示した原子間距離roで引力と斥力は釣り合って0になる。ポテンシャルエネルギー(位置によって変化するエネルギー)もこの位置で最低になり安定する。この距離で原子は結合している。 原子の間隔が大きい場合も合力は引力側であるので,お互いに近づくような力が作用していることになる。従って,原子が離れていても安定化のため近づくようになる。 |
|
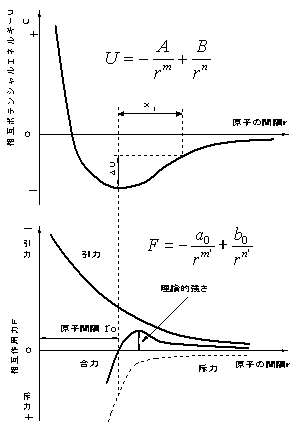 図1 相互ポテンシャルエネルギー,相互作用力と原子間距離の関係 |
|
| 図1の原子の間に作用する力FとポテンシャルエネルギーUの式はコンドン−モース曲線(Condon
- Morse curve)と言われている。 結晶性物質において、加えられた外力が作用して、一次結合(イオン、共有、金属結合のいずれの場合も)の復元力が生ずることを図1の原子間距離と相互作用力の関係曲線は示している。 |
|
| ■ | 原子間距離roから外力によりわずか変位するとき |
| roから曲線の接線を引くと、ro近傍では曲線と接線がほとんど一致する。この部分が弾性変形である。材料の強度と破壊のページで述べているように、図2の最大値が材料の引張りに対する理論強さを表すことになる。 | |
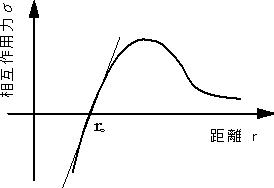 図2 弾性変形 |
|
| ■ | 外力と内力 |
| 2つの原子の間で、原子間距離roで引力と斥力は釣り合って0になる。外部から力を加えて、この位置から、原子をずらし、原子間距離をro+Δrとro−Δrとしたときの復元力の方向を調べてみる。弾性変形では、「はじめての材料力学」でも述べているように、2つの原子はバネでつながれている場合と同じように考えることができる。 | |
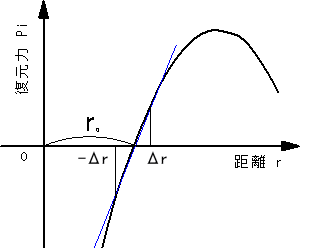 図3 |
|
| ●外力が作用しない場合 原子間距離roに相当し、バネは自然長で、復元力は生じない。 |
|
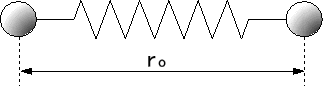 (a)外力が作用しない場合 |
|
| ●引張りの外力Pが作用する場合 原子間距離をro+Δrとなり、元の位置roに戻そうとする復元力Piがバネの内部に生ずる。2つの原子間の場合も同様である。この復元力を一般に「内力」と呼んでいる。外力Pと復元力Piの大きさは等しく、向きは反対である。単位面積当たりの大きさで表せば、応力(stress)であり、「はじめての材料力学」で説明している材料の抵抗力である。Δrが大きくなり、復元力が図3の最大値を超えると限界の値であり、材料は破壊することになり、このときの抵抗力の大きさが引張に対する材料の理論的強さである。しかし、材料力学では弾性範囲であるので、図3で曲線が接線とほぼ同じ程度のΔrの値の範囲で扱う。 |
|
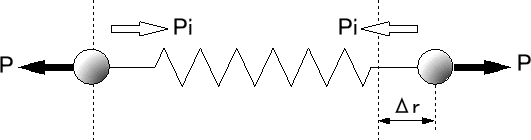 (b)引張りの外力Pが作用する場合 |
|
| ●圧縮の外力Pが作用する場合 原子間距離をro−Δrとなり、元の位置roに戻そうとする復元力Piがバネの内部に生ずる。引張りの場合と同様で、復元力の向きが異なるだけである。 |
|
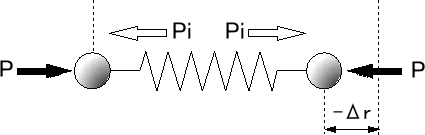 (c) 圧縮の外力Pが作用する場合 |
|
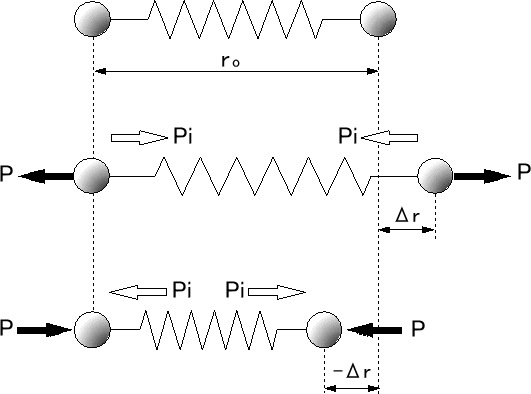 (d) 図(a),(b),(c)の関係 図4 2つの原子の間に生ずる復元力 |
|
| ここでは、引張と圧縮変形の場合について述べたが、せん断変形の場合も同様に説明することができる。 |