有効数字について

■

有効数字と測定値の取扱い

　
　測定値の取扱いで大切なことは，計算では（特に電卓）大きな桁数になっても，実際に数値として意味のあるデータとするためには何桁までの数値を取るかと言うことである。良く、電卓で計算された数値をそのまま全桁を書くとかExcelで計算された値をそのまま書く方をよく見かける。技術者としては非常識であるので注意が必要である。

(1).有効数字と計算
　
　3.249と言う数字は純数学的には 3.249000･････という意味であるが，測定値の場合は，末尾の数値が四捨五入されて 9 になったと言う意味で，測定値Ｍは次の範囲にある。
　　　　　　　　　　　　　　　　　　3.2485　≦　Ｍ　＜　3.2495
このようなことから一般には，測定値は末尾の数値までが意味があり，それ以下の桁については不明である。このように意味のある数字を『有効数字』という。また，測定値においては，例えば目盛りを有する測定器で測定する場合，目分量では最小目盛りの1/10まで読むことができるのであるから，最後の桁の数字は目分量で読んだことを意味する。従って，そのひとつ前の桁は最小目盛りの位置を表すことになる。

　　【測定値の例】計測器で測定し、例1から例５の値を得たとする。

例	1	L＝ 12.3 mm	有効数字	3桁
例	2	L＝ 12.300 mm	〃	5桁
例	3	L＝ 0.0034 mm	〃	2桁
例	4	L＝ 1200　 mm	〃	4桁
例	5	L＝ 2.34 × 10⁴ mm	〃	3桁

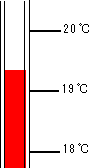
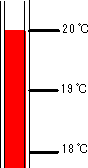
　例３のように，小数点以下の桁数を表す０は有効数字には数えないが，例4のような場合の0は有効数字に数える。例4で有効数字が2桁である場合は，例5のような表現を用いて，1.2×10³ mm のように書くべきである。特に、単位換算して０が入ってくるときは注意すべきである。

【測定例】　1℃の目盛りを有する温度計での測定
　
　図1(a)の場合は、最小目盛り1℃であるからアルコールは19℃と20℃の目盛りの3分目当たりに達している。従って、温度19.3℃。0.3度は目分量による読みで有効数字3桁。

　　図1(b)の場合は、20℃の目盛りと一致する。目分量は0である。従って、測定値は、20.0℃となる。測定値の場合、20℃と読むのは間違いである。測定値20℃は，10℃の目盛りの温度計で読んだ結果と解釈される。1℃の最小目盛りの温度計と10℃の最小目盛りの温度計で測定された測定値はどちらが誤差は少ないかは言うまでもない。このように、目分量では最小目盛りの1/10まで読むことが可能である


(a)	(b)

図1　温度の測定

　
　また，例1と例2を比較すると，数学的には同じ値であるが，測定値の場合は意味が異なる。例2の12.3 mmにおける「3」は目分量で読んだ結果であり，「2」は，最小目盛りの位置を表すので，1 mm の最小目盛りを有する測定器（例えば物差し）で読んだことになる。例3の12.300 mmにおける最後の「0」は目分量の読みの結果ちょうど「0」であり，その前の「0」は最小目盛りの位置を示し，0.01 mmの最小目盛りを有する測定器（例えば，ﾏｲｸﾛﾒｰﾀ）を用いたことを示している。誤差は、最小目盛りの1/10より小さい値となる。
　誤差百分率は分解能を測定値で割った値で、1.23と12.300場合は下記のようになり

　有効数字が多いほど、分解能が高いほど、誤差の入る割合は小さいことがわかる。
　
(2).測定値どうしの計算
　有効数字の異なる２つ以上の測定値を用い，計算してある量を得るときの有効数字の扱い方である。
利害関係のある場合は，JISで取扱いが定められている。ここで示す方法は便宜的なものである。
　
●加減の計算
　小数点以下の有効数字の桁数を揃えるようにする。小数点以下の有効数字の桁数の最小のものより一つだけ多くとって計算し，最終結果は測定値の中で小数点以下の有効数字の桁数の最小のものに揃える
　

さらに、この値を使って、計算を続けるときは、24.64を使う。
*有効数字３桁（16.5による。小数点以下の有効数字１桁）

●測定値どうしの剰余計算
　測定値の中で，有効数字の最小のものに着目し，このものより一つ多い桁に揃えて計算し，最終結果は有効数字の最小のものに合わせる。　誤差百分率が大きい測定値に影響を受けるからである。

【計算例１】すべての数字が測定値であるとする。

　
＊0.078の有効数字は2桁で、3桁目は読むことが不可能。読めない値が384792に入っている。試しに，読むことが出来なかった有効数字3桁目を9とおき，0.0789として計算してみる。
　　　　　　　　　　 0.0789 × 26.8 × 1.028=2.1737266
となり，有効数字3桁目は，7に代わっている。読めないはずの9が影響していることになる。このような意味で384792は無意味な数字と言うことになる。計算結果は，有効数字の小さい測定値(誤差百分率が大きい測定値)に影響を受けることがわかる。
　次のように計算する。
◆最小有効数字:　測定値の内の最小有効数字に着目，他の測定値はこれより１桁多く取って計算

*1.028は，四捨五入して，有効数字3桁に丸めてしまう。

【計算例２】
　上降伏点の荷重P_uy=4.81×10³N，d₀=12.021mmの時，上降伏応力の計算。最小有効数字は荷重値の3桁。

　重力加速度，円周率などは，最小有効数字より1桁多くとって計算する。最終的に，最小有効数字桁数＋１の値を四捨五入するからである。
　　　　　　　　
【計算例３】
　　　l₀=80.00mm，l_f=106.45mmのとき，伸びφを計算する。最小有効数字は4桁。

　＊ %の100は測定値ではないことに注意。
　
　以上は，実験などで使用する測定値に関する有効数字の取り扱いであるが，利害関係が伴う場合はJIS規格で定める「数字の丸め方」に従うことになる。