「はじめての材料力学」サポートページ >モールの応力円について

モールの応力円について

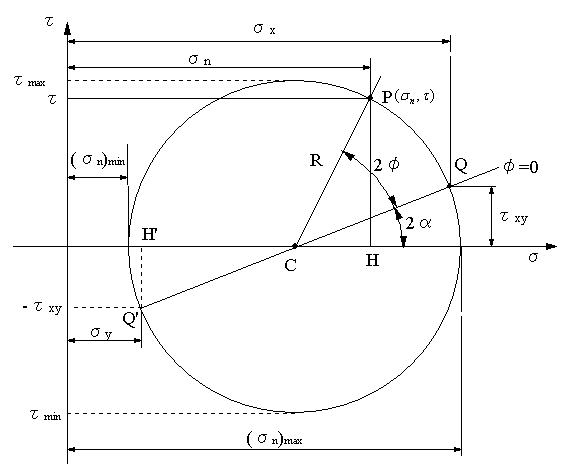
図1のように、教科書1)１章から7章までの知識から、平面応力の応力解析の結果、微小部分に、ｘ方向にσｘ，τｙｘ，ｙ方向にσｙ，τｘｙが生じている。図2のように、x軸と断面の法線がφの角度をなす断面上に生ずる垂直応力σｎと，せん断応力τを計算をして求め、それらの最大値、最小値と最大値が許容応力以下になるように部品の形状や寸法を決定する。 　安全な設計をするためには、それらの最大値、最小値と最大値、最小値の生ずる位置を知る必要がある。 　σを横軸に、τを縦軸に取り、垂直応力σｎと，せん断応力τの関係式を表すと円の方程式となり、作図する事が出来る。これが モールの応力円である。 作図した図から数値を読んで計算しなくても、最大応力値やそれらが生ずる面を図面から簡単に知ることができる。例えば、図面で、10mmを10MPaとして、後述の値を得て、円をプロットし、φ、α等の値から、図面上の値を測定すると応力の最大値、最小値などやそれらが生ずる面を知ることが出来る。 　以前，三角関数の値は，三角関数表から求めるしか方法がなかったので，作図法は便利であったが，電卓の普及とともに三角関数の値が簡単に得られるので，垂直応力等の値は，直接計算した方が精度も良く、効率的である。しかし、モールの応力円は貴重な発想法として評価されている。

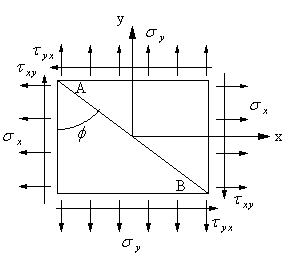
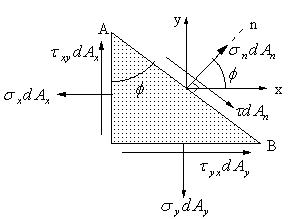
図1　微小部分に生ずる応力 図2　微小部分に生ずる力

図3　モールの応力円

解析の結果、σｘ，τｙｘ，σｙ，τｘｙが数値で与えられる。グラフ用紙を準備し、横軸に垂直応力σｎ，縦軸にせん断応力τ軸を取る。応力値の大きさに応じて、単位長さ当たり、何MPaにするか決める。例えば、10mmを10MPa。円の半径R、中心C、角度αを計算式で求める。グラフ用紙に円とQQ'線を引く。QQ'線と2φの角度をなす円の中心を通る線を引き、円周と交わる点をPとすると、角度φをなす断面上に生ずる垂直応力σｎと，せん断応力τはP点の座標値で与えられる。垂直応力σｎと，せん断応力τの最大値と最小値は図3に示す長さを測定し、応力に換算することによって得られる。

はじめての材料力学」サポートページ >モールの応力円について