いろいろな荷重が作用した場合について,材料中に生ずる応力を計算によって求め,その値が許容応力以下であれば安全として寸法と形状を決めてきた。許容応力を決めるとき、用いた材料の強さとしては,あまり変形が許されない場合は降伏応力,多少の変形が許される場合は引張り強さを採用した。
実際に稼働する機械や装置の設計の際には,使用される環境条件下で強度として何を採用するか考慮すべき点は多い。例えば,原子炉の一次冷却水と二次冷却水の間で熱交換を行うステンレス製の細管は、つねに脈流する高圧すなわち荷重が繰り返し作用する、また、高温状態、腐食条件下で使用され、さらに放射線の影響を受けながら稼働していることになる。すなわち、材料が低温,高温あるいは腐食環境下で使用され、さらに放射線に常にさらされている。
金属の結晶の物理的や機械的性質は、高温、腐食環境、放射線環境では変化するのが普通であり、さらに,これらの複合条件下で使用される場合には,材料はその性質を,通常の場合と異なり,一般に,強度を低下させる方に変化する。従って、設計技術者はこれらの現象を考慮した上で設計することが必要になってくる。このような複雑な条件下においては,材料の強さとして,降伏応力と引張強さを採用することは,安全性に問題が生ずる。設計の立場から,このような複雑な条件を把握し,対応する使用材料の”適切な強度”を選択するためには、あらゆる環境下における材料の性質の変化を理解する必要がある。
材料の物理的性質、化学的性質の研究は、物理学や化学および物性学の分野であり、結晶の構造などは金属学の分野であり、機械的性質の研究は、材料力学、構造力学の分野が関係してくる。また、複雑な環境条件下での性質の変化を明らかにするためには、原子の程度の大きさ(微視的)の視点から、目に見える寸法の大きさ(巨視的)の幅広い視点からの研究が必要となる。このように、いろいろな学問分野を有機的に結びつける必要があるために生まれた学問が材料科学(Materials Science)である。
材料科学は、工学、理学はもちろん、医学の分野にまで必要とされている材料に関する総合学問である。多くの材料のうち、金属材料がもっとも多く使用されている材料であり学問も進んでいるので、金属を例に、金属の機械的性質(力が加わったときに示す性質)を解釈するのに必要な基本的知識について述べる。詳細は、材料科学の参考書、あるいは
ホームページ(http://ms-laboratory.jp/strength/st_top.htm)を参照されたい。
金属は金属結合しており、原子が立体的に格子状に規則正しく配列した結晶構造である。この構造が,光沢がある、電気を通す、熱伝導がよいなど”金属らしい性質”を生むことになる。
この原子構造はX線の回析によって明らかになった。結晶内の原子間の距離は2.5 Å(オングストローグ 1cmの1億分の1)程度であり,1cmの線上には約4,000万枚の原子の面があることになる。
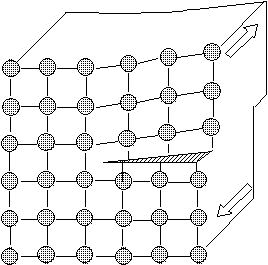
付図C.1に体心立方構造(Body-Centered Cubic Latice)、すべり面、すべり方向を示した。立方体の各隅と中心に原子が並び、単位胞は9個の原子より構成される。実際は、隣接する単位砲と共有することを考慮すると単位胞に属するのは、二つの原子と言うことになる。BCC金属は、室温の鉄、W、Cr、Moなどが代表的な金属であり、FCCと比較すると変形しにくい金属である。
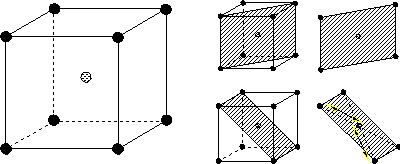
付図C.1 体心立方格子(BCC)構造とすべり面、すべり方向
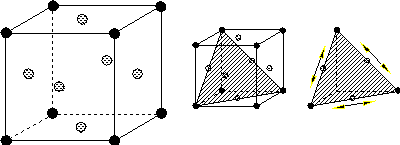
付図C.2 面心立方格子(FCC)構造とすべり面、すべり方向
付図C.3 引張変形 付図C.4 せん断変形
付図C.5の場合、2つの原子をxだけ引き離すのに要する応力σは
σ=σc sin(2πx/λ) (C.1)
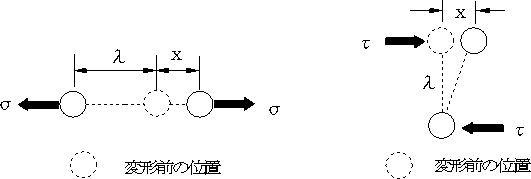
付図C.5 2つの原子の間に働く力 付図C.6 格子の変形
σc= E/10 (C.2)
のように求められている。Eはヤング係数である。
一方,付図C.6の場合も,同様な方法で,原子を元の位置からxだけ横にずらすのに必要な応力τは
τ=τc sin(2πx/λ) (C.3)
で近似され,せん断応力τをだんだん大きくしてゆき,最大値τcを越えた後は小さな応力で移動し,となりの原子の位置におさまる。付図C.5の場合と比較すると,垂直応力の時は,原子の結合の強さσcを越えてしまうと元に戻らず破壊するが,せん断の場合,原子的な結合は一時的に切れるが,となりの位置に入ったときは元の安定な原子の状態になる。結果的に,上下の原子が1原子だけずれたすべりが生じ,結晶全体からみてもすべりの結果,段差ができることになる。このτcが理論的せん断強さで,近似的に,
τc =G/2π (C.4)
付表C.1に引張に対する実際の材料の強さ(実測値)とまったく欠陥がないとして計算した理論値との比較を示した。 付表C.2では、せん断に対する材料の強さと計算した理論値σc,τcの実測値は,理論値の1/100ー1/1,000になっている。この差は何から生ずるのであろうか。理論計算では,結晶格子は理想的に完全な状態,格子欠陥などの欠陥がないことで話を進めてきた。実際は,格子欠陥,空孔や介在物による欠陥が多く含まれ,それらによる応力集中効果によって外荷重は小さくとも,材料の内部では大きな応力が生じ,σc,τcを軽く越えると言うことが起こるからである。
また,金属の精製過程は勿論,溶接などの加工によっても欠陥が入り込む。結果的に,材料の強さが欠陥の存在によって著しく低下することになる。欠陥がなければ理論的な強さに近づくことが予想される。種々の欠陥の中で,特に結晶格子の面状の欠陥である転位(dislocation)が材料の強度に大きな影響を及ぼす。
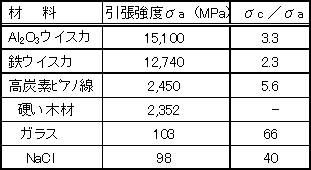
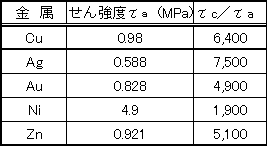
*付表C.1、付表C.2は、横堀武夫著、「材料強度学」、岩波全書より引用
1934年にイギリスのテイラー(G.I.Taylar)は結晶は完全ではなく,転位(dislocation)という原子配列の乱れ,面状の格子欠陥が存在し,この転位による結晶のすべり機構を提案した。この転位の考え方によって、金属の現象をほとんど説明できるようになった画期的な考え方である。
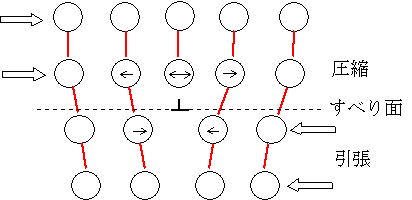
付図C.7,付図C.8のように,あるところから原子面が欠落しているところが転位である。正の転位は、Tの記号で表し、縦の線が余分な原子面を表している。負の転位はこの線が逆になる。付図C.9の破線は、乱れた原子面の境界、すべり面(余分な原子面の下端が移動する面)であるが、この境界よりも上側の原子面は原子が余計に詰められた状態(圧縮状態)、下面の原子は、格子間隔が引き伸ばされた状態(引張)にある。図中の矢印は原子が本来の位置に移動したい方向を示した。余分な原子面にある原子は、どちらに転んでも良い状態(不安定平衡)にあり、後述のように、小さなエネルギーでどちらに移動できる状態にある。
付図C.7 刃状転位 付図C.8 らせん転位
けっきょく,対になっている上下、2原子間の結合を切るのに必要な大きさのせん断力τは小さなものになり、わずかのせん断応力を与えれば,転位(余分な原子面は)は簡単に1原子間隔だけ右に移動することになる(付図C.10)。これを結晶の端から他端まで1原子づつ、順次繰り返すと結晶は1原子だけすべったことになる。式(C.2)では,一度に全部の原子の結合が、切れるとして計算した。転位を移動させるのに必要なせん断応力τは、欠陥のない結晶を移動させるのに必要なせん断応力τcの大きさよりかなり小さくなることが理解できる。
付図C.9 転位の周りの変形
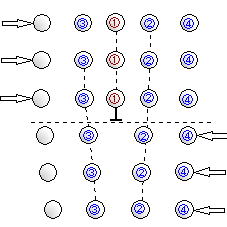
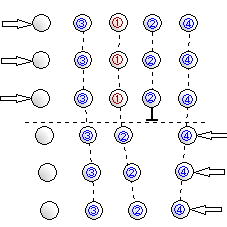
(a)移動前 (b) 移動後
図C.10 転位が1原子間隔だけ移動
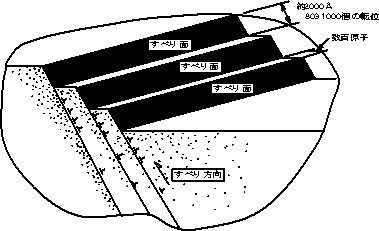
実際に金属がすべった表面を観察してみると、すべり量は、付図C.11に示すように約2000Åであり、これは800ー100個の転位が移動したことに相当する。フランクとリードは、増殖機構を考え、実験で証明した。付図C.12において、ABは転位線(付図C.12の刃状転位で刃先の部分である)であり、ABはすべり面に乗っている。他の破線の部分はすべることができない面に乗っている。
ABは紙面に平行にせん断応力が作用すると転位は移動する。A、B点は移動できないので転位線は膨らむ。次第に輪は大きくなって成長する。せん断応力に対して、垂直な部分が刃状転位、平行な部分はらせん転位、中間的な部分は両者の混合である。
付図C.11
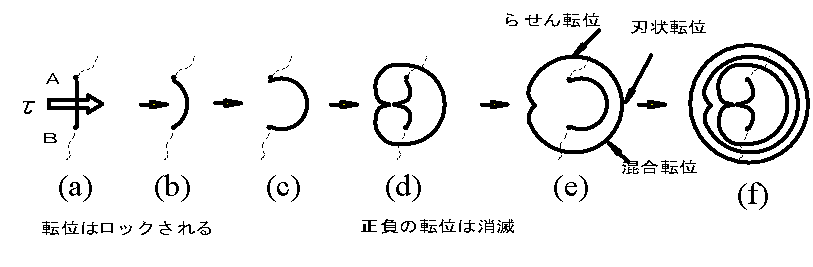
付図C.12
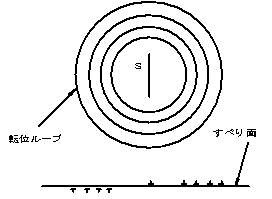
付図C.13 転位ループの断面
転位の移動→転位の増殖→多数の転位が同一すべり面上において発生。この多数の転位が障害物にじゃまされ、移動できないときどうなるか。転位の移動を阻止する障害物としては、実験観察の結果、結晶境界、金属中に含まれる非金属介在物、転位などであることが分かった。
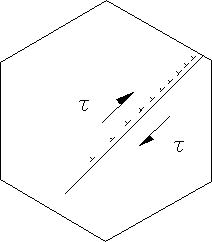
付図C.14,付図C.15に、刃状転位が結晶境界や介在物によって移動が阻止される様子を示した。刃状転位の場合、正の転位と負の転位(余分な原子面がすべり面の下方にある。)が出会うと消滅するが、同じ符号の転位が近づくと、ますます格子のゆがみが増大するので、お互いに反発し合う。
外力と転位同士の反発力と障害物から受ける力が釣り合い、結果として、障害物自身に大きな反力が生ずる。この力は、集積した転位の個数nに比例し、付図C.15に示した方向に大きな垂直応力nσが生ずる。これが転位の集積による応力集中である。
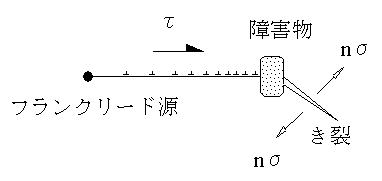
付図C.14 結晶境界への転位の集積 付図C.15 障害物への集積による応力集中
応力集中が生ずると、材料自身の本来の強度以下の負荷応力ですべりや破壊が生ずることになり、材料の強度が低下したことになる。ぜい性破壊、疲労破壊、応力腐食割れなどにおいては、このような局部的な転位の応力集中が破壊の起点となる場合が多い。
以上のように,欠陥の存在による応力集中のため,材料内部では予想を越える応力(安全係数で余裕を持たせた許容応力の何倍もの)が局部的に生じ,その箇所では,降伏応力や引張り強さ以上になっていることが考えられる。
欠陥の存在が本来の材料の強さ(欠陥のない理想的な材料の理論強さ)を低下させ,このような値を示しているのである。従って,材料を強化する基本的な方法としては,①転位等の欠陥を全く無くするか、②転位の活動を阻止し,転位が小さな力で転位が動かないように,転位を動きにくくして、すべりや転位の集積による応力集中を起こりにくくすればよさそうである。
転位はよく焼きなました鉄でも,1c㎡当りに含まれる転位の個数(転位密度と言う)は,106~108(100万ー1億)個ほどである。転位の平均間隔はおよそ,1~10μm(ミクロン = 1/1000 mm),原子が4,000~40,000個くらい並んでいると,転位が1個存在する程度である。従って,計算上では直径を0.01mm以下にすれば転位が1本も入らない材料ができそうである。ウイスカーはこの程度の大きさの直径であり,セラミックスのウイスカーは,ほぼ理論的な強さに近い強度を有することがわかった。ウイスカーは髪の毛よりも細いのであるからそれらを束ねて高分子材料などと複合させて使用される。これらを応用した実用材は、カーボン繊維、ボロン繊維などと高分子材料を複合させた複合材料である。
転位の下の原子間隔は通常よりも引き伸ばされているのであるから,エネルギー的に不安定であるので,付図C.16に●印で示すように、炭素や窒素等の小さな原子を侵入させ補ってやることによってエネルギー的に安定化させるものである(コットレルの転位のくぎづけ)。
このような転位は、簡単には移動することができず、結果的に強度が高くなる。合金による強化の一つである。鉄に炭素を少量合金した炭素鋼はこの代表例である。炭素鋼の上降伏点ではくぎ付作用から転位が解放されることを意味し,いったん解放されると低い応力(下降伏応力)で転位は移動することができるようになり,すべりが生ずる。
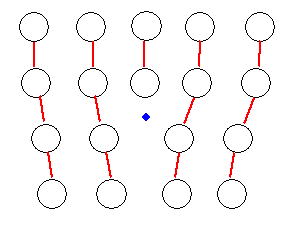
付図C.16 転位のくぎ付け、・ は、炭素や窒素等の小さな原子
刃状転位は、付図C.6の正の転位(余分な原子面がすべり面の上方にある)と負の転位(余分な原子面がすべり面の下方にある)が出会うと消滅するが、同じ符号の転位が近づくと、ますます格子のゆがみが増大するので、お互いに反発し合う。この性質を利用して,金属を塑性変形させ,転位の増殖機構によって転位を大量に増やしお互いの反発力の作用とお互いに障害物になるなどで転位を動きにくくする。これがひずみ硬化による材料の強化方法の原理である。
その他として、単結晶の場合は、すべり方向は結晶中どの領域においても同じであるが、多結晶の場合、各々の結晶粒は格子の向きが異なり、すべり面も異なる。最大せん断応力方向と一致した結晶粒が、まずすべりを開始するが、その他の結晶粒はすべりに対しては抵抗となる。結晶粒が小さいほど抵抗となる結晶が多くなる。付図C.14に示すように、結晶が小さくなるとすべり線も短くなり、集積する転位の数も少なく、結果的に応力集中が小さくなる。したがって、結晶粒を小さくすれば強化されることになる。
単結晶に引張り荷重を加え,徐々に荷重を大きくしていくと,軸方向と45度をなす面上の最大せん断応力も大きくなる。結晶構造によってすべることのできる面(すべり面)と方向(すべり方向)が決まっていることは前に述べた。多結晶の場合、各々の結晶粒はすべり方向が異なり、最大せん断応力方向に近いすべり面上の転位が,移動可能な大きさのせん断応力に達すると,まず,すべり面上を移動を開始する。転位は増殖されその数を増す。1個の転位が結晶の端まで達すると1原子間隔分のずれ(すべり)が生ずる。多数の転位が通過した場合は転位の数の分だけのすべり量が生ずる。すべりが生じた結果,金属表面にはすべり線と断層ができる。これが『金属のすべり変形』である。
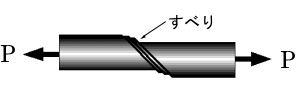
図C.17 試験片に生ずるすべり
