| たわみの重ね合わせ |
| 梁のたわみは、荷重が数種類作用する場合はかなり複雑な計算になる。このような場合、1つの荷重が単独に負荷される場合についてたわみの式y=y1(x)を求め、別の荷重が単独に負荷される場合についてたわみの式y=y2(x)を求めて、両荷重が同時に作用した場合、たわみy= y1(x)+y2(x)で表すことができる。これを"たわみの重ね合わせ"と言う。 |
| (1).両端支持、1つの集中荷重の場合 −−−一般的な解法 |
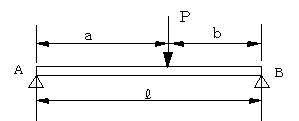 図1 |
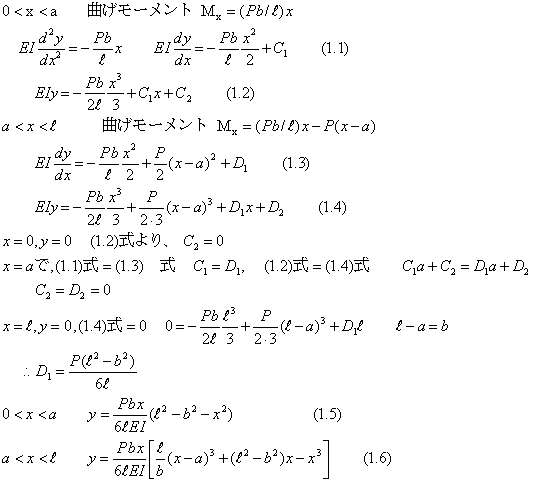 |
| (2).両端支持、2つの集中荷重の場合 −−−一般的な解法 |
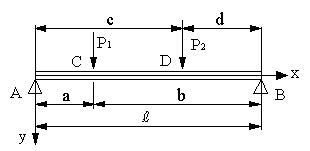 図2 |
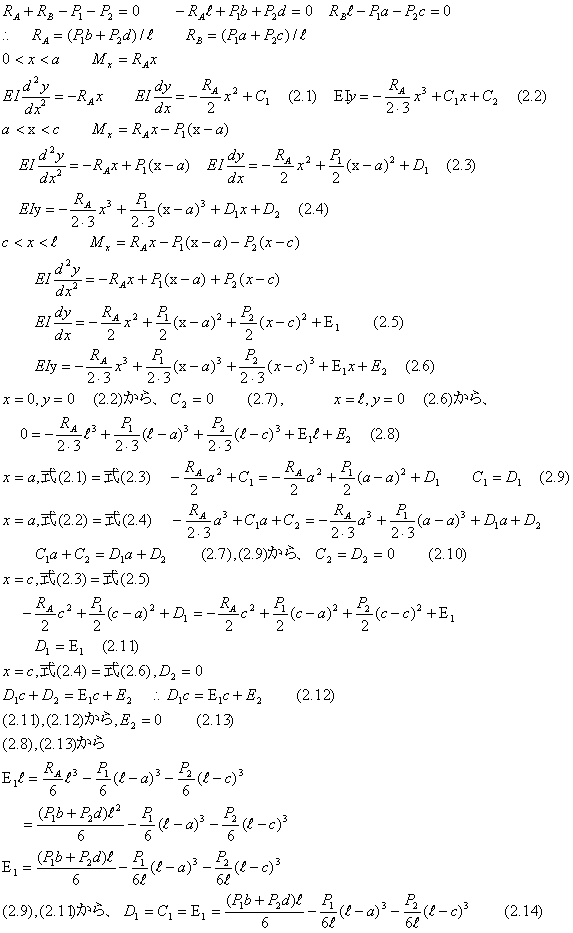 以上の計算をまとめると次のようになる。 |
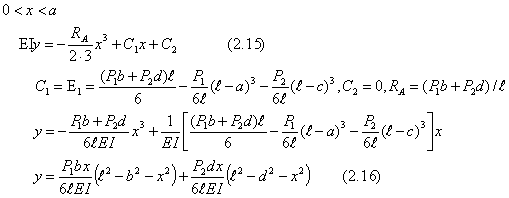 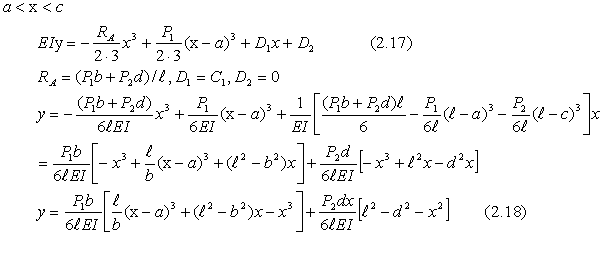 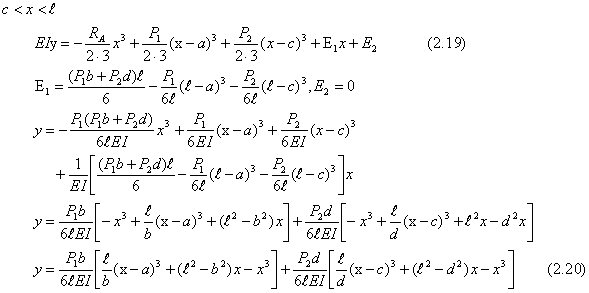 かなり複雑な解法になることが解る。この点において、次に述べる重ね合わせ法により、幾分、簡素化される。 |
| (3).両端支持、2つの集中荷重の場合 −−−たわみの重ね合わせ法 |
| 下記の式は、式(3.1),(3.2)において、P1→P2,a→c,b→dに置き換えた式が、それぞれ(3.3),(3.4)である。定義区間においてこれらの式を加えれば図2のP1、P2の荷重が同時に作用する場合のたわみの式が求まる。 一般的な解法と比較すると、たわみの式は同じ結果であることが解る。 |
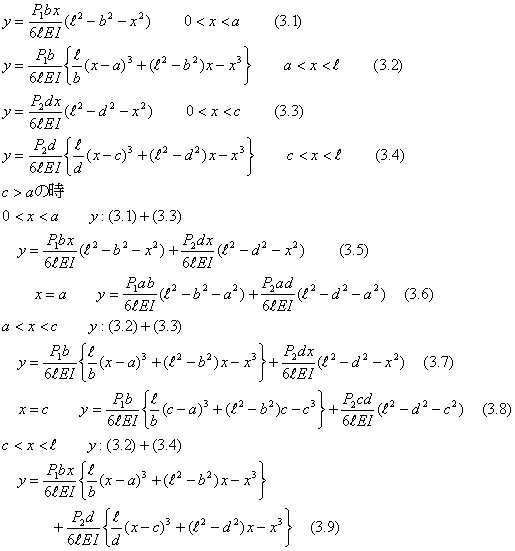 |