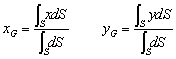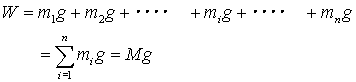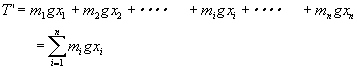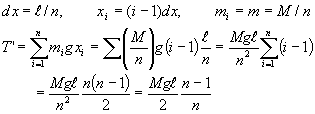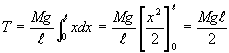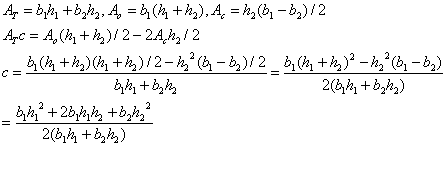重心の求め方について
|
物体を構成する微小部分には,その質量に比例した重力が鉛直下向きに作用します。各々の微小部分に作用する重力は平行な力であり、各々の微小部分に作用する力を合成した合力が物体の重さであり、合力の作用する位置が重心です。物体の全重量を重心に集中させたと考えても良い。物体の形状が決まれば重心は定点です。
均質で厚さが一様な薄い板や、断面一様な細い針金などは、その重力の大きさが面積や長さに比例する。このように、物体の形状だけから決まる重心のことを図心と言います。
均質な物体の場合、体積V,密度ρ,重力加速度gとすると,重量w=ρgVであり,重力の大きさは体積に比例します。さらに,均質で厚さtの一様な板が水平におかれた場合は,重力の大きさは面積Sに比例する(V=tS,w=ρgtS, dV=tdS)から次の式ようにかける。この場合,厚さ一定であるから、2次元平面で考えることができる。 |
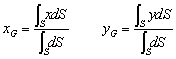
|
■平行力の合成の応用 ---重心の位置を求める場合
|
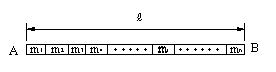
水平に置かれた棒をn個の部分に分割する。 分割された物体の各部分に作用し、分布している重力は、方向が同じ(鉛直下向き)で、平行である。この力を合成し、1つの合力にまとめたとき、この合力の作用線の位置が重心である。
合力の大きさWは、前述の結果から,物体の質量Mとおくと |
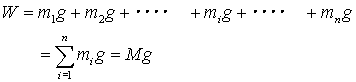 |
Aに関するモーメントT’は、図8(a)と図8(c)の場合に等しくなることが必要(合力の説明の項参照)があるのでモーメントを求める。
|
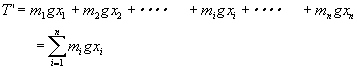
|
 |
 |
| (a) n個の部分に分割 |
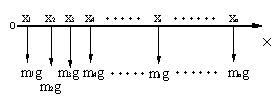
(b) 分割した部分に重力が作用 |
|
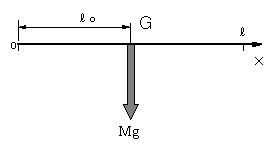
| (c) 重力を合成 |
| 図 合力の作用する位置が重心G |
|
| 簡単にするために,n等分の時、 |
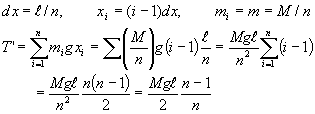 |
| 極限値を求めると重力によるモーメントの総和T’は |
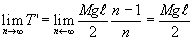 |
となる。
同じ重力によるモーメントの総和T’を求めるのに,積分法を利用して求めてみる。
微小部分dxに作用する重力は,単位長さ当たり(M/l)gであるから、dxの部分には,(M/l)gdxの重力が作用する。A点からの距離x、この部分のモーメントΔTは、
|
| ΔT = (M/l)gdx・x (区分積分法のAi) |
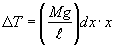 |
| 上式を0からlまで積分を行う(区分積分法,Aiの和をとり、極限値を計算に相当)と |
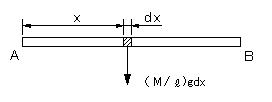 |
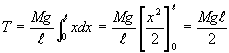
|
なる。一方、W(=Mg)によるモーメントMAは、作用点l0
と置き
MA = W・l0
力を合成しない時のモーメントの大きさと合成した力によるモーメントの大きさは等しい,T=MAから、
|

|
となる。作用点l0 が重心の位置で、断面が一様な棒の場合は中点である。
|
■T型の場合
|
図形の形状が、重心の位置が既知の図形に分解できるときにはそれぞれの面積と位置から合成することにより全体の形状の重心位置が求められます。これは、力の釣り合いとモーメントの釣り合いの原則から求まります。
平行力の場合は、力を合成したり、分解したりするとき、力の効果が変わらないためには力とモーメントが同じになる必要があります。
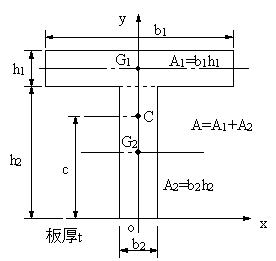
例えば、T型の場合は2つの長方形から成り、厚さが一様とすれば、各部の重さは面積に厚さ、比重を掛ければ重力になります。T型の重心位置は、図の原点に関する重力のモーメントが、2つの長方形に作用する重力の原点に関するモーメントの和に等しいことから求められる。
|
●2つの長方形から求める場合
|
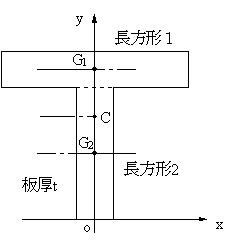
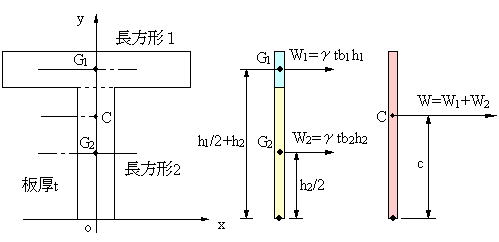
| 図の場合、長方形1と長方形2の重心の位置は既知であり、G1,G2となる。ここに、面積に対応する重力が作用する。これらによる原点に関するモーメントの和が、T型の重心Cに作用する重力によるモーメントと一致することから、重心cの位置を求めることが出来る。 |
|

|
|
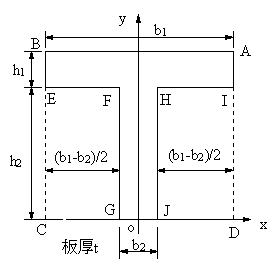
| ●T型の空白部に作用するモーメントを差し引いて求める場合 |
| ABCDの矩形の重心に作用する重力によるモーメントから、 ERGCとHIDJ の重心に作用する重力によるモーメントを差し引いてT型の重心位置を求める。 |
|
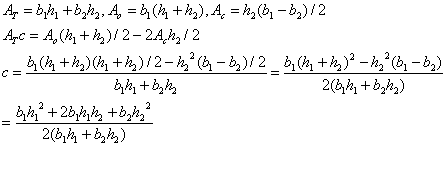 |
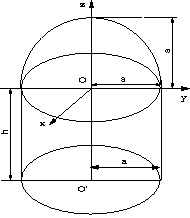
| ●立体図形の場合 |
図のように、密度1.3g/cm^3、半径a=18cm、高さh=24cmのエポキシ製円柱に、密度2.7g/cm^3、半径a=18cmのアルミ製半球を図のように接着した。この連結体の重心(xG,yG,zG)を求める。ただしz軸を円柱の軸に一致させ、x,y面を接着面上にとる。
この場合も、xz面を水平に取り、y方向に重力が作用するとして、前述の方法で問題を解く。
|
|

|
 |