| 「はじめての材料力学」サポートページ >6章補足楕円形断面の断面二次極モーメント |
||||||
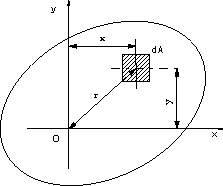
| 楕円形断面の断面二次極モーメントJ、x軸、y軸に関する断面二次モーメントIx.Iy |
||||||
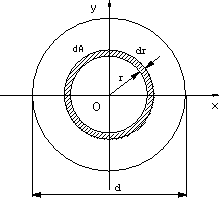
| 直径d、半径dの円の中心を通り、断面に垂直な軸に関する円形断面の断面二次極モーメントJは次のように求められる。 図1のように中心からrの距離にある幅drのリング状の微少部分の面積はdA=2πrdrであるので、r2を掛けて、0からd/2まで積分する。(1)式から、対称形であるので、Ix.=Iy であり、x軸、y軸に関する断面二次モーメントは(3)式のように求まる。 |
||||||
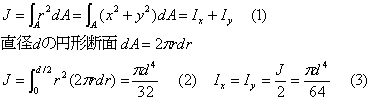 |
||||||
|
||||||
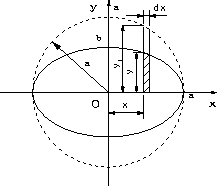
| 長軸a、短軸aの楕円形断面の断面二次極モーメントJはx軸、y軸に関する断面二次モーメントIx.Iyを求めて、(1)式のように和をとる。 Iyは微小面積dAが(4)式のようになり。断面二次モーメントの定義式に代入すると(5)式のようになる。x軸より上の半分の部分を計算し、2倍している。この積分は、文献の公式集を参考にしている。積分結果は(6)式となる。同様にIxは式(7)のようになり、断面二次極モーメントJは(8)式のようになる。 |
||||||
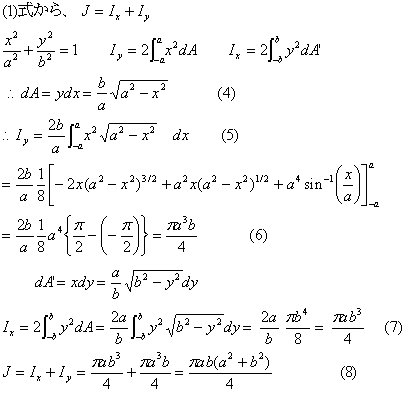 |
||||||
| 一般の教科書では、楕円形の場合、図3で円形断面から高さy1をb/aの比に減少したとして断面二次モーメントを求めている場合が多い。おそらく、余り使われない、無理関数の積分を使うのを避けたためと思われる。ここでは定義に従って無理関数の積分を使った。 |
||||||
| 参考文献 | ||||||
| *森口、宇田川、一松、「数学公式Ⅰ 積分微分・平面曲線」、岩波書店 このシリーズはⅢまで発売されており、大学院などで理論解析を行うときは手元にあると便利である。 |