|
1. はじめに
稼働中にある機械や構造物を構成している部品や部材は経年変化を生ずるのが一般的である。機械や構造物の破損事故において、腐食が関与している場合が多い。石油タンクなどは、腐食損傷が生じた場合,不連続的に板厚を測定し,減肉量が決められた値に達した時、その部分を交換するという方法をとっている。破損事故にいたる破壊は,本来、確率的な現象である。このような現象においては統計処理を行い,寿命を評価する極値統計の方法は不可欠である。機械や構造物の寿命を適切に予測できれば、それらの安全管理に益するところが極めて大である。
また、局部腐食を受けた材料は、強度が著しく劣化することが明らかになり1)、補修のための交換時期を決定する必要がある。
ここでは、この極値統計方法を石油タンク底板の残存寿命推定に適用する方法を述べ、実際に長期間使用され、腐食孔が底板を貫通し、油が漏洩した石油タンクから切り出した試料の板厚測定データに極値統計の手法を適用し、その残存寿命が実際と一致し、有効な方法であることを示す2)。また、これらのデータをパソコンで処理し、寿命推定、χ2検定を自動的に行うプログラムを製作し、これについても概要を述べる。
2. 極値統計の理論とその方法
2.1 腐食現象について
腐食現象は、その損傷形態から、均一腐食と局部腐食とに大別される。均一腐食が平均値問題に属するのに対して、孔食・すきま腐食・応力腐食割れ等の局部腐食は、極値問題に属する。石油タンクの底板から発生した多数の局部腐食のうち、最も深く進行し、材料の肉厚を貫通するまでの時間がその材料の寿命となる。石油タンク底板の寿命を考える場合に、局部腐食の深さに関して、その最大値が問題になる。
2.2 腐食現象の極値分布について
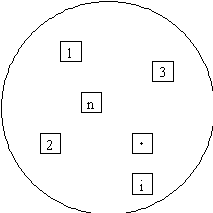
今、ある石油タンクの底板の裏面腐食の最大値を推定する事を考えてみる。板厚を超音波厚さ計等により測定し,初期板厚から計測値を引き,この値を腐食量とする。計測は全面を計測するのではなく、一定面積をもつ領域(例えば,1m×1m)の領域をn箇所選び、それぞれの領域から得られるデータからタンク底板全面積における最大腐食量を推定することを考える(Fig.1)。
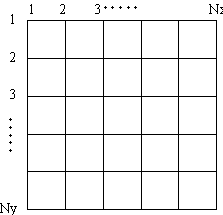
それぞれのサンプル領域の腐食分布状態は、Fig.2のように規則性のある格子点(Nx×Ny)における腐食量Xi(j)に関するヒストグラムによって近似的に表される。実験結果1)によれば、実際に腐食を受けたタンクから切り出したサンプルの同一領域において,データの採取位置間隔を変えて測定したもので,横軸は腐食量の代わりに板厚,分布が格子の取り方に依存しないことを示している。Nx×Nyとして,49,100,500,400の4通りの場合について測定し、100点程度測定すれば,分布形状は同様な様相を呈することが判明した。すなわち、Xi(j)に関するこの分布形状は試料の腐食量の特性を表していると考えてよい。この分布は極値解析において、基本分布と呼ばれる。Xi(j)から求められる最大値をUiとすると、Ui=(Xi(j))max となり、n箇所の領域を同様に測定すると、このような値がn個得られることになる。最大値Uiの集まりは、基本分布とは別の分布に従う。これが極値分布である。実際には、測定領域を分割し、それぞれのグループの中の最大値を抽出し、最大値のデータの集まりに対して極値分布の統計処理することになる。
|
||
|
||
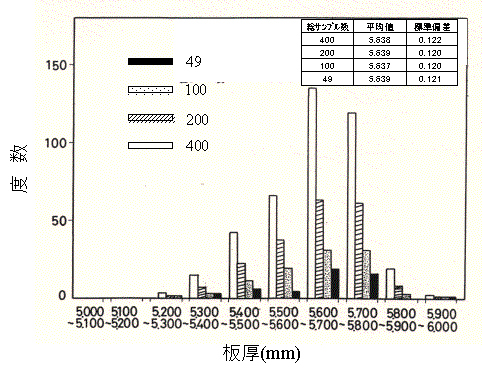 Fig.3 サンプル領域の板厚分布 |
||
| 2.3 二重指数分布の適用の判断
二重指数分布は、Gumbel分布とも呼ばれている。これには,最大値分布と最小値分布がある。局部腐食による損傷おいて一番問題となるのは、その最大侵食量、それによる装置の最小寿命の予測であることに対応している。
最大値分布FI(x)、最小値分布F−I(x)の式は次式によって与えられる。
FI(x)=exp[−exp{−(x−λ)/α}]
F−I(x)=1−exp[−exp{−(x−λ)/α}]
それぞれの密度関数は、
fI(x)= (1/α)・exp[−(α−λ)/α−exp{−(x−α)/α}]
f−I(x)=(1/α)・exp[(α−λ)/α −exp{(x−α)/α}]
で与えられる。ここで,α、λは位置パラメータ,尺度パラメータと呼ばれ,α>0である。密度関数が導かれる過程において、xが大きい領域で基本分布が指数分布となることが仮定されている。極値解析を行う場合、基本分布が不明であっても手続き上不都合はないのであらかじめチェックする必要はない。ただし、最大値のデータが推定された二重指数分布に適合しているかどうかは検定によって確かめることになる。
|
||
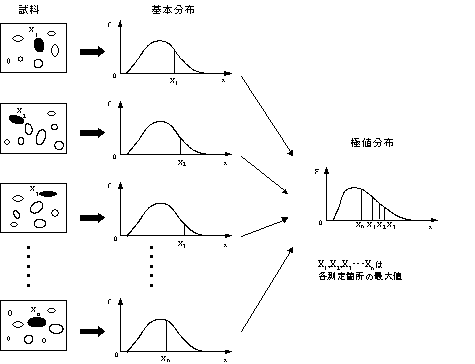 Fig. 4 基本分布から極値分布へ |
||
| 2.4 二重指数確率紙を利用したタンク底板の寿命推定
二重指数確率紙は、最大値分布FI(x)の両辺の自然対数を2回とると
ここで,
とおくと
となることから、直交座標系の1軸に
を目盛り,他の一軸に確率変数xを目盛った方眼紙である。縦軸にFI(x)、横軸にxにとり、データをプロットして,直線のまわりのばらつきが一定の範囲内にあれば二重指数分布に従っていると判断される。この直線からパラメータα、λを求める。
2.5 寿命推定の手順
ここでは、実際のデータを用いて、寿命推定の手順について述べる。
実際に腐食孔がタンク底板を貫通し、油が漏洩した箇所の近傍から切り出した試料をポイントマイクロメータを使用し、肉厚測定をした。タンクの仕様を表1に示した。試料数は23個で、測定領域は10mm×10mmとし、測定箇所は1mm間隔の格子点に相当する点で、1試料の総測点数は100点である。23個のデータのグループの最大腐食量を求め、これらの最大板厚減少量を0.05mm毎にクラス分けをして、その度数を示したものが表2のfi である。これから、計算によって底板に腐食貫通孔が生ずるまでの時間を推定することになる。寿命に達した材料であるから、寿命推定計算結果が0になればこの寿命推定方法が有効であると言うことになる。
|
||
Table.2 最大値の度数分布 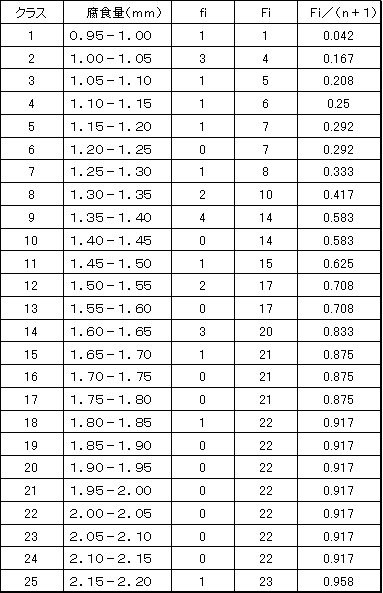 |
||
|
以下、これらのデータを用いた手計算による寿命推定の方法を示す。プログラムの計算手順はこの順序に従うことになる。
(1).累積度数Fiの計算
最大値の分布を検討する場合、度数(fi) を小さい方から累積し、Fi を計算する。
(2).累積分布Fi/(n+1)の計算と二重指数確率紙へのプロット
累積度数(Fi)を試料個数nに1を加えた値(n+1)で割って累積分布(Fi/(n+1))を算出する。nはデータ数である。結果をTable.2に示した。これを二重指数確率紙に、x軸上に腐食量を目盛り、各クラスの上限値をx値とし、Fi/(n+1)をFI(x)値としてプロットする。
(3).直線の式の係数の決定
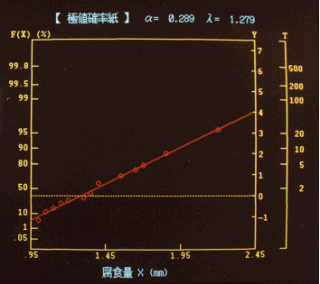
プロット点に対して、ばらつきが最小になるように直線を引き、確率紙のグラフから、切片と傾きを求め、直線の式を決定する。データ例の場合は、傾き3.4573、切片の値4.426が得られた。
(4).パラメータλ,αを求める
縦軸y,横軸xと置くと、y=3.4573x−4.426が求められたので、(2)式の係数を比較することにより、データ例の場合は、α=0.289、λ=1.253が得られた。分布関数FI(x)は、データ例の場合は、
FI(x)=exp[-exp{-(x-1.253)/0.289}] (3)
となる。
(5).寿命予測の方法
1つのサンプル領域から,1個の最大値uが得られる場合に、ある値aより大きな値が得られるまでには何カ所の領域について調べることになるのかを考えてみる。今,この数をNとすると、その確率はP(N)は次のようになる。はじめから(N−1)箇所までのuのそれぞれがaより小さい確率がF(a)であるから、(N−1)箇所すべてにおいて、aより小さい確率はF(a)N−1である。N番目の領域で、uがaより大である確率は{1−F(a)}である。従って、
P(N) ={F(a)}N−1・{1−F(a)} (4)
Nの期待値Tは再現期間である。
F<1であるから
T=1/{1−F(a)} (5)
となり、確率紙におけるT目盛りとF(x)目盛りの関係は(1)式の関係がある。
次にTを設定する。今考えている全底板を対象領域に考えると、次式が成り立ち、データを適用すると次式の結果となる。
T=(全低板面積)/( サンプル領域1つの面積)
= (π/4)・D2/(10×10)
= 5,772,300
ただし,タンク直径D=27.11m、測定領域は10 mm×10 mmである。
Tに対応するx(xmaxとおく)を求めると、
式から
となり,T>>1であるから,
T=577230,λ=1.253を上式に代入すると、xmax=5.473が得られる。
残存寿命をZ[年]とすると、
Z=(残存板厚)/(腐食速度)
=(to−t)/Y
= 0.0025 年
ここに、初期板厚to=6.0 mm、現状の最小板厚(xmax)、t=5.473、タンクの使用年数Y=15年である。
(6).推定された確率分布の妥当性の検討
これまでに述べたような方法で、推定された二重指数確率分布が実測値を表しているものであるか否かを判定する必要がある。
|
||
Table.3 確率分布の理論値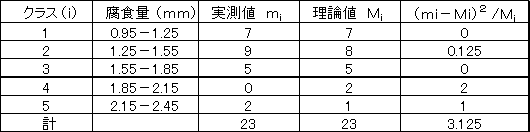 |
||
| ここでは、χ2検定を得られた結果に対して適用する。いま、ある母集団からのサンプル値とそれから推定した確率分布による理論値が表3のようであったとする。このとき、
をつくると,Mi≧ 5であればχ2分布に従うとしてよく,確率変数x(=χ2)おけるχ2分布の確率密度関数は
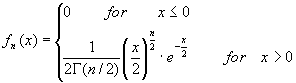
であり、nは自由度である。
f(x)に、ある値aをとり、上式に代入すると、
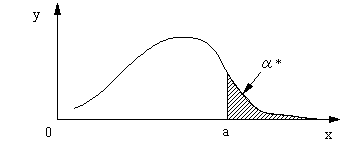
Fig.5
α*はχ2値すなわち、xがaよりも大きい確率を与える。このα*が十分小さく、(a≦x)とすると、そのようなx値が発生することはまれであり、miは実測値であるからxがaより大きくなってしまったのは、Miすなわち推定した理論値に問題があったわけである。すなわち、理論式が適切ではないと判定される。この判定内容はα*の値によって左右される。α*は危険率あるいは有意水準と呼ばれる。
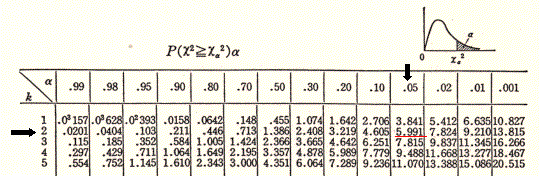
ここで,上記の方法で推定された二重指数分布が実測値を表しているかどうか判断するために、このデータの場合のχ2検定を行う。Table.3のmi値はTable.2ではfiとして示した。計算の結果、χは3.125となった。ここで、χ2 分布表を参照することになるが、自由度kは、k=(クラス数−パラメータ数−1)であるから、k=5−2−1=2 となる。有意水準*を5%とすると、
χ=3.125,a=5.991
となり、χ<aである。従って二重指数分布(3)式は5%の危険率で棄却されない、すなわち二重指数分布の仮定は正しいと言うことができる。
Table 4 χ2 分布表
|
||
|
3.寿命推定プログラムの概要
3.1 使用言語
寿命推定のプログラム作成に使用した言語は、Microsoft BASIC Professional Development System Version 7.1(以下、MS-BASIC )である。MS-DOS用のQuick Basic、Windows用の Visual Basicの上位バージョンに相当する。この言語の特徴について述べる。 (1).構造化プログラミングが可能
(2).独立実行型ファイルにコンパイル可能
(3).ツールボックスとして、豊富なライブラリーが用意されている。
(4).ラージモデルが可能
(5).MS-DOSシステムコールが可能
3.2 プログラムの基本的仕様
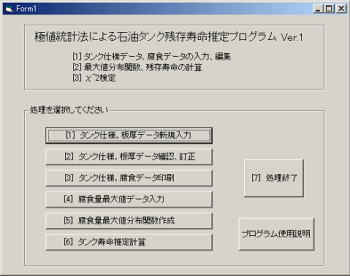
数値入力の回数が多いため、キーボードを押す回数をできるだけ少なくし、また、数値入力以外はマウスで処理できるようにした。またボタン箇所は、マウスの移動量をできるだけ少なくするよう配慮した。 入力事項は、すべてアラート画面にて確認、再入力できるようにし、入力ミスを回復できるようになっている。入力、選択はすべてウインドウを利用しているので視覚的に満足できる。MS-BASICはEMSなどの機能を利用できるので、インタープリターでも処理速度はかなり高速である。
プログラムは、データ入力部,データ訂正確認印刷の処理部、基本統計量・寿命計算・検定部、ファイル管理からなる。
(1).諸データ入力部
タンク解放点検時に、腐食の度合いを調べるため通常、超音波厚さ計にて板厚を測定する。測定間隔は、消防法により決められているが、しかし、側板とアニューラー板のT型溶接部の応力集中箇所あるいは目視により、腐食予想される箇所などは、特に綿密に、30mm程度の間隔で測定される。解放点検時の測定で得られるデータは一般的には、板厚量、座標点である。また、あらかじめ、区画を設定し、測定するので、グルーピングをする必要があることは少ない。
いずれにしても、求めたい量は腐食量であり、測定板厚データの1グループの中の板厚最小値(初期板厚からこの値を引いた量、すなわち腐食量最大値)が必要となる。従って、1番目の区画の板厚データの入力後、1番目の区画のデータ集合の腐食量最大値を検索、さらに2番目の区画のデータ入力後、データ集合の中の腐食量最大値を検索のような手順で、N個の区画の腐食量最大値を求める。
a.手入力
板厚値と測定点座標の手入力、腐食量に換算後、入力した全データ、腐食量最大値、最小値等のデータ情報を1区画につき1データファイルとしてMS-DOS形式でディスクに出力する。データは、腐食データ、位置データ、1区画の最大値、最小値、タンク仕様である。全データ入力の後、全区画の最大値を抽出し、最大値データファイルを作成する。
b.データファイルからの入力
測定器からデータがディスクに記録されている場合は、ディスクから読むが、あらかじめ指定された形式に他のプログラムで変換する必要がある。
c.板厚最小値の入力
消防法により、5年に一回の開放点検が義務づけられているが、タンク検査データは、諸機関に報告されているものがほとんどであり、この場合、報告書には、区画ごとの最大値、最小値が記載されている。この場合は、このデータを入力することによって直接、腐食量最大値データファイルが得られることになる。
d.タンク仕様データの入力
解析しようとするタンクのデータで、形式、容量、初期板厚等である。このデータは文字データとして処理し、必要なときに数値に変換する。
(2).データ訂正・確認・印刷の処理部
入力したデータの訂正、確認、追加、印刷などの処理を行う。
(3).基本統計量・寿命計算・検定部
腐食量最大値の度数分布の作成、基本統計量の計算、寿命計算、χ2検定の処理を行う。
度数分布の区間の幅、確率紙へのプロット、横軸の表示範囲、目盛り間隔等はすべて、事前に指定できるようになっている。確率紙に相当するグラフのプロット画面と最小二乗法によって得られた直線の式の係数から計算されたα、λの値の画面に表示する。なお、χ2分布表はデータファイルとして別個準備されており、有意水準、自由度を入力すると、χの値が表示される。
(4).ファイル管理
開発したプログラムが、ハードディスク、ディスケットなどに大量に蓄積すると内容の判別が大変であるので、ディスクドライブ、ディレクトリ、サブディレクトリに存在するファイルのコメントをあらかじめ記入し、必要に応じてファイル内容のコメントを一覧できるプログラムを作成した。内容を記述したコメントの他に、ファイルの種類、作成年月日、更新されているかどうかが一覧できる。また、一覧表を印刷可能である。これらの管理ファイルは、@FCP.DATのファイル名でディスクやディレクトリに置かれる。
3.3 汎用ルーチンの開発
Visual Basicでは、マウスによってウインドウの大きさやボタンの位置を決定し、それぞれのテキストをその位置に画面を見ながら入力し、確認しながらウインドウを設計できるが、MS-BASICの場合は、サブルーチンの引数に位置、大きさ、テキスト、ボタンの機能等を与える形式になっている。画面設計は簡単であるが、いずれのBASICも、イベントが生じた後の処理プログラムの作成は必要である。
数値入力以外はすべてマウスで選択できるように、煩雑に使用するルーチンを作成したが、(4),(5)以外のルーチンは、Visual Basicでは比較的プログラム作成を意識することなく簡単に画面設計できる。
4.手計算とパソコンによる計算結果
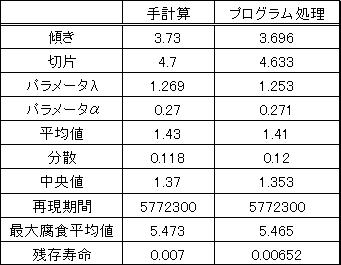
手計算による結果とパソコンによる計算結果をTable. 5に示した。手計算では、直線は、目分量で引いているので若干の差が現れている。
Table. 5 計算機結果と手計算の比較
|
||
|
5.まとめ
実際に石油タンク底板として長期間使用され、腐食によって貫通孔が底板に生じ、オイルが漏洩したタンクから採取した試料のデータに、極値統計によって残存寿命推定を行った結果、残存寿命、0.0025年と言う値が得られ、極値分布の統計解析による残存寿命の推定は、腐食損傷において有効な手段であると言える。
また、手計算では、かなり膨大なデータのため処理が大変であるので、パソコンを用い、処理することによってかなり省力化ができる。最近は、板厚測定のデータはフロッピーディスクに記録されるようになったことから、データフォーマットが一致すれば、測定終了とともにタンクの残存寿命が判明することになる。
大型石油タンクの場合、消防法により5年ごとの解放点検が義務づけられているが、t開放点検時毎の測定データにこの寿命推定方法を適用すれば残存寿命の推移が確認でき、石油タンク等の腐食による経年変化を生ずる構造物の保守上かなり有効な手段となることが期待できる。
現在は15年間の使用期間に行われた3回の定期点検時に得られたデータを解析中である。多くの測定データにこの方法を適用し、この方法の信頼性をさらに確認する必要がある。
参考文献
1) 小山,亀井:日本機械学会講演論文集,No.802-2(1980),146
2) 小山、「極値統計法を用いたタンクの寿命評価」、委託研究報告書(東電工業(株)),1995.
■各量の計算式
(1) 中央値 δ
FI(x)=0.5 におけるxがδであるから,
(2) 最頻値 xm
dfI(x)/dx=0となるxがxmである。(3)式から、xm=λが得られる。すなわち、位置パラメータはfI(x)のピーク値のxに等しい。
(3) 平均値 μ
とおくと,
(γ=0.57721:Eulerの定数)
(4) 分散 V
|
||
| 残存寿命推定プログラム |
||
|
||
| 極値統計関連ページ 極値統計については下記の著書に詳細に記載されています。すでに絶版と思いますが、腐食防食協会のホームページで多少の情報は入手可能です。 「装置材料の寿命予測入門―極値統計の腐食への適用 」、腐食防食協会 |