図1に示す、梁の断面ABCDには荷重に抵抗してせん断力Vxとモーメントが生じている。簡単な長方形断面について考察する。断面が正方形の柱状の微小部分mnはZ軸に平行で、この微小部分に生ずるせん断応力は同じ大きさで、柱状の4面で生ずるせん断応力τは同じ大きさで、左端で示しているように、いずれの面に生じているせん断応力の大きさは等しく、共役せん断応力になっている。このせん断応力の状態については、教科書(はじめての材料力学、1.6)で学んでいる。微小部分の表面y=±h/2ではτ=0で、他の面上のτ=0である。中立軸から上面、下面に向かうに従って減少する。
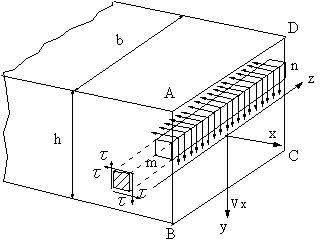
図1
この部分の底面bdxは梁の底面と一致しているので、応力は生じない。上面pp1は中立面に平行で、任意距離y1距離だけ離れ、この高さにおけるせん断応力τを受けている。
この部分の両側の端面は図2(b)に示す影をつけた梁の断面の一部であらわされる。これらの両端面pn,p1n1はx軸に平行な曲げ応力σを受けている。この部分を自由物体として取りだしたものを図2(c)に示した。もちろん、両端面pn,p1n1に平行にせん断応力τが生じているが、ここではx方向の平衡だけを考えるので関係なくなる。
最後に、曲げモーメントが両端面pn,p1n1で、MからM+dMに変化する場合について考える。

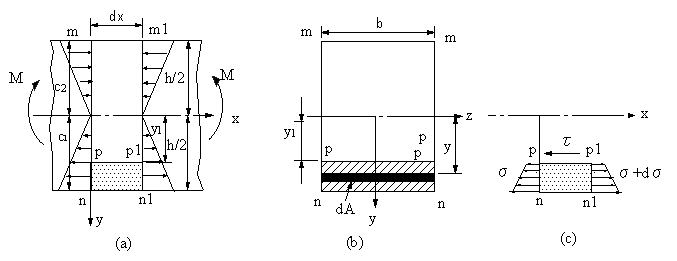
図2
図3