金属材料学分野の解説トップページへ>金属と結晶構造

従来の機械・金属材料学分野の解説
材料科学講義のプレゼン資料から
1.　 金属と結晶構造

	■材料科学　Materials Science　材料学の新しい分類と統合
	材料科学を構成する主な分野 　・固体の力学･････材料力学，応力解析 　・物性　 ･･････････結晶学，金属物理 　・熱力学，統計力学　･････相変化，熱処理，固体間の反応 　・電子物性･････半導体，電子材料 　・確率・統計学　 　材料の性質の変化は、原子の程度の大きさ（微視的）の視点から、目に見える寸法の大きさ（巨視的）の幅広い視点からの研究が必要となります。このように、従来のいろいろな学問を有機的に結びつけ、より信頼性のある強度や機能性を求めるために生まれた学問が材料科学(Materials Science)です。
	■材料の分類 　・金属材料　・高分子材料（プラスチック）　・セラミックス材料 　・半導体材料　・流体材料 　・複合材料　２つ以上の材料を各材料の長所を生かして複合 　　Ex.FRP :ガラス繊維（直径0.01mm）とﾌﾟﾗｽﾁｯｸ(PC,ｴﾎﾟｷｼ等) 　・バイオテクノロジーによる生体由来の材料 　 材料の役割による分類 　・機能性材料　ある機能を有する.　　　半導体，ｾﾝｻｰ材料、抗菌・消臭材料 　・構造材料　　力が作用するところに使用される。　機械や構造物に使用される材料， 　 ■材料の工学における立場と特徴 　 (1).あらゆる工学の分野で材料関係の科目が置かれている。 　　機械工学，電気工学，土木工学，建築工学など 　　 (2).新材料が開発されるとき、技術革命が起こる 　　・半導体　　　　電子機器，コンピュータ　 　　・セラミックス　高温ガスタービン　　高温燃焼(1500℃)，高効率　 　　・ｾﾝｻｰ材料　 ロボット　　視覚，触覚，温度，匂い等の識別　 　　・CD,MD,DVD 　　・セラミックスエンジン（開発中）　　効率が現在の２倍、約50%に 　　・環境浄化材料 (3).エネルギー関連システムにおける使用環境 　　　・高温、高圧、低温、腐食環境
	工業的に大量に使用されており，生ずる現象が原子の程度の尺度で説明できるほど理論化されている金属材料を主として述べる 　　　　　　　　　　　 (1).金属と結晶構造　　　　　 (2).金属の変態と合金の構造 (3).相律と二元系の平衡状態図　　(4).炭素鋼の基礎　 (5).炭素鋼の熱処理
1.1	原子の構造と金属結合　---- 材料の微視的構造
	すべての原子は，正の電荷を持つ陽子と電荷を持たない中性子から構成される原子核とその周りを回る負の電荷を持つ電子から成り立っています。陽子の＋電荷と電子の−電荷が釣り合っています。原子核を中心に一定の規則性のある決められた軌道上を電子は回っていて，軌道は電子殻と呼ばれ，原子核を中心として幾つかの段階に分かれており，それぞれの殻に存在できる電子の数は決まっています。原子の大きさ　10-8cm,(=1Å)である。、周期律表の０族の原子が，それぞれの殻に配置できる電子の最大数であり，安定な配置です。これらの原子は，電子が軌道上にいっぱいの状態で，他の原子と電子のやりとりはなく，結合したりしません。安定していない原子は，一番外側の電子(最外殻電子)を出したり，他から取り込んだりして，安定な状態，０族と同じ電子数になろうとします。 　 　原子の結合は，NaClのように，Na+，Cl-　の２つのイオンの静電気的な力で結合するイオン結合，２つの原子の最外殻電子が両原子のみ共通な電子軌道を動き，お互いに共有することで安定な最外殻電子数になり強固に結びつく共有結合があります。金属の場合は，外側の電子が、各原子から飛び出し，それらが互いに手を取り合って原子を結びつけている金属結合です。２原子間だけでなく，原子全体に共有されるのが特徴で自由に電子が結晶中を動き回るのでこの電子を自由電子と言います。金属らしい性質はこの自由電子のために生まれます。例えば，光が当たって粒子が金属内に入り込もうとしても自由電子にはじかれるために金属光沢を持ちます。熱や電気を通しやすい性質もこの自由電子によるものです。 　その他、ファン・デル・ワールスによる結合は原子が弱い分極を起こし，原子間に電気的引力で結合しています。
1.5	金属と結晶構造
	金属の結晶は規則正しく３次元的に原子が整列し、金属結合をしています。結合の仕方から金属は、強いという性質が生まれます。
	図1.1金属の結晶構造
	鉄(Fe)原子の大きさは，2.52オングストローム(Å，１オングストロームは１億分の１センチ)，隣接する原子との間隔も同じ値であるので，鉄の上に長さ1cmの線を引いたとき，線上には約4000万個の原子が存在することになります。従って，1cm3の立方体の中には天文学的な数の原子が含まれ，規則正しく並んでいます。その中の少数の原子の並び方を知ることができれば，その金属の全体の配列を論じることができます。 　 　最も基本となる配列を基本単位格子と言います。特徴を表す最小単位の構造，単位胞(unit cell)を考えます。図1.2のように直方体の各隅に原子が配置し，立方格子の場合はa = b = c です。
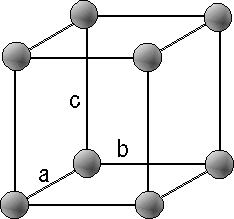	図1.2　unit cell
	次に，代表的な３つの結晶構造について述べます。
■	体心立方格子 Body Centered Cubic Lattice, B.C.C
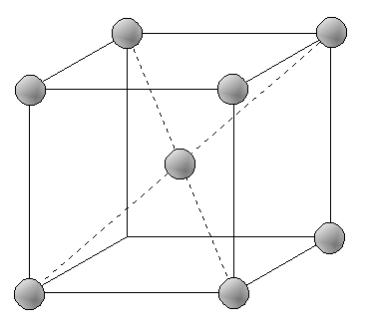
	体心立方格子(Body Centered Cubic Lattice．略して，B.C.C)の単位胞は，図1.3のように，立方体の各隅とその中心に原子が1個配置し，９原子で構成されています。立方体の１辺の長さを格子定数と言いますが，長さa = 2.78Åです。原子は，実際には各原子球が接触し合う状態で模式図を図1.3(b)に示します。原子は，-273℃でほとんど静止していますが，温度が高くなるにつれて，(a)で示した位置を中心として振動し，室温では振動しています。このため，温度が上昇すると熱膨張を生じます。密度は0.68で，室温の純鉄α-Fe, W, Cr, Moが代表的金属で，比較的変形しにくい金属です
	(a) (b) 図1.3 体心立方格子
■	面心立方格子 Face Centered Cubic Lattice, F.C.C
	面心立方格子(Face Centered Cubic Lattice,略して F.C.C)の単位胞は，図1.4のように，立方体の各隅と各面の中心に１つの原子が配置し，14個の原子で構成されています。 密度は0.74で，Au, Ag, Cu, Pt, Al, Ni, γ-Fe(高温の鉄)等が代表的な金属です。変形しやすく箔に加工できる金属です。
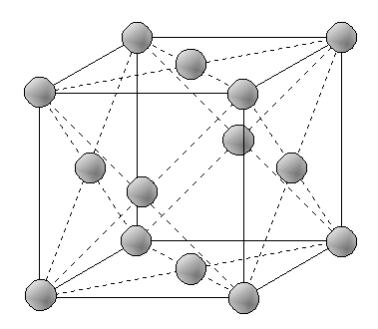	図1.4 面心立方格子
■	稠密六方格子 Hexagonal Closed-Packed Lattice, H.C.P
	稠密六方格子(Hexagonal Closed-Packed Lattice, 略してH.C.P)の単位胞は，図1.5のように原子が並んでいます。密度は0.74で、面心立方格子の場合と等しく、性質も似かよっているが、面心立方格子より変形しにくい金属です。。代表的な金属は、Mg, Zn, α−Zr等である。
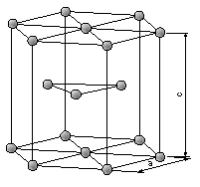	図1.5 稠密六方格子
1.6	結晶面および結晶方向の表示法
	原子が並んでいる面，原子面は1つの結晶内で多数の異なった面が考えられる。原子面上での原子の密度や原子間の距離など異なるため，原子面あるいは結晶面によって性質が異なる。実際に，それぞれの結晶面と結晶方向における物理的性質,電気的性質，力学的性質等が異なる。例えば力が作用したとき，変形のため原子が移動しやすい面や方向が存在する。金属の結晶の性質を論ずる場合，結晶面や結晶方向を表示することが必要になってくる。
■	面ABCの決め方
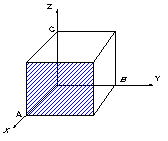
	A，B，Cにある原子を含む結晶面ABCを考える。図1.6のように単位胞のX,Y,Z軸方向の単位長さ(格子間隔)を，それぞれ，a，b，cとする。OA，OB，OCは，格子間隔の整数倍の長さとなるので 　　　　　 OA=α･a , OB=β･b , OC=γ･c　 　α，β，γは，＋，−の整数で，例えばＸの正方向＋ ，負方向−とする。
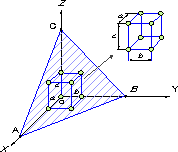	図1.6　結晶面ABC
	このα，β，γの逆数の比をとり，次式に示すように，整数化し，簡単な整数比h：k：lで表す。
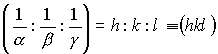	( h k l ) を面ＡＢＣの面指数，ミラーの指数と名付ける。
	【例題１】　図1.7の斜線の面，立方格子の場合 　立方格子の単位胞の場合 a=b=c であり，y軸とz軸に平行であり，無限遠で軸と交わると考え，β= ∞ ,γ=∞とおく。 　　　　　OA=1･a , OB= ∞･b , OC=∞･c α=1,β= ∞ ,γ=∞を定義式に代入して 　　(1/α):(1/β):(1/γ)=(1/1):(1/ ∞ ):(1/ ∞ )=1:0:0 　　　∴ (h k l)=(100)
	図1.7 図1.8 図1.9
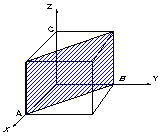
	【例題２】　図1.8の斜線の面 　単位胞の場合 a=b=c、OA=1･a , OB=1･b, OC=∞･c(z軸に平行)， α=1,β=1,γ=∞ 　(1/α):(1/β):(1/γ)=(1/1):(1/1):(1/ ∞ )=1:1:0　 ∴ (h k l)=(110)
	【例題３】　図1.9の斜線の面 　　単位胞の場合 a=b=c、OA=1･a , OB=1･b, OC=1･c， α=1,β=1,γ=1 　　(1/α):(1/β):(1/γ)=(1/1):(1/1):(1/ 1 )=1:1:1 　　 　　　　∴(h k l)=(111)
■	結晶学的に性質が等しい等価な面表し方
	(100),(001), (010)は，結晶学的に性質が等しい 　　　　　　　　↓ 　　　　　　等価な面 　　３つの等価な面を指すとき　{100}　と書く
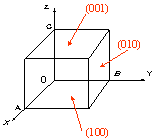	結晶内の方向は，図1.11に示すように，結晶軸の原点を通る考えて，その直線上の任意の一点の座標で示す。図の場合，座標(ua,vb,wc) のとき，方向は[uvw]で示す。
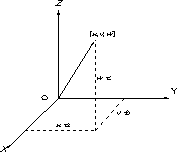	図1.11
	本来、材料力学の初歩的な知識も解説する必要がありますが、この部分は「はじめての材料力学」で解説していますので、これをご覧下さい。
	＊金属材料学の講義に補足説明として使用したプリントの資料とOHPのプレゼン資料からです。使用した教科書、矢島、市川、古沢、「若い技術者のための機械・金属材料」、丸善．　金属材料の基本を学ぶのにデータも豊富で最適な教科書です。

　　　　

金属材料学分野の解説トップページへ>金属と結晶構造