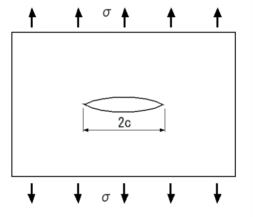
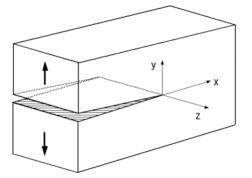
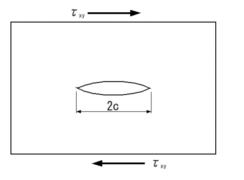
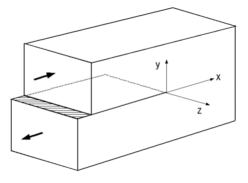
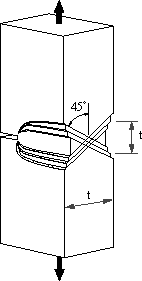
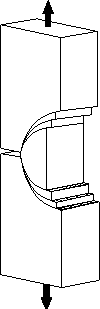
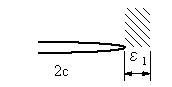
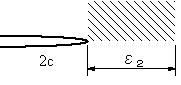
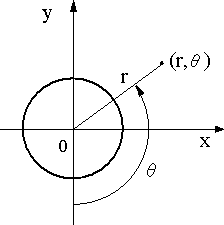| 1.き裂を有する材料のき裂開口の変形様式 き裂を有する弾性体に外力が作用する場合、長さ2c、高さ2b、き裂先端の曲率半径ρのき裂が板に存在する。変形形式は図1~3のように、き裂に対する荷重の作用の仕方から、3つのモードに分類されている。 |
||||||||||||
|
||||||||||||
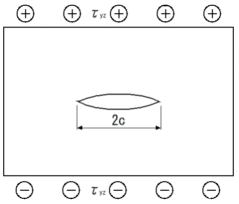
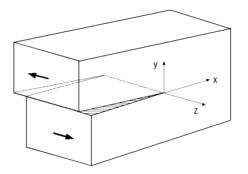
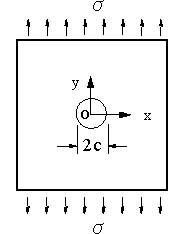
| ■モードⅠ 引張形式 引張応力がき裂面に対して垂直に作用する場合である(図1)。図でZ方向の応力は変化しない平面応力かZ方向のひずみが変化しない平面ひずみ状態を取る。 ■モードⅡ せん断形式 外応力はせん断応力でき裂面に対して平行に作用する(図2)。平面応力か平面ひずみ状態をとる。 ■モードⅢ 面外せん断形式 外応力はせん断応力であるが板厚方向に作用する(図3)。 2.切欠やき裂先端近傍の応力状態 ■円孔と楕円孔の場合 弾性体の無限平板に半径cの円孔が存在し、図4のように無限遠で一様な引張応力σが作用している場合で、円の中心を座標点の原点に取り、中心からの距離rとrがy軸とのなす角θとすると次式のように応力が求められている。 |
||||||||||||
|
||||||||||||
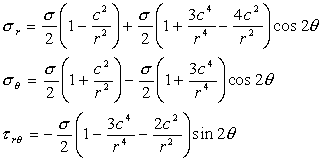 (1) (1) |
||||||||||||
| 式(1)でr=c, θ=π/2とr=-c、3π/2で、σθ=3σとなり最大値を取り、3倍の応力集中となる。 長軸2c、短軸2bの楕円孔の場合は式(2)のように求められている。 |
||||||||||||
ただし、曲率半径ρ=b2/c の関係がある。 |
||||||||||||
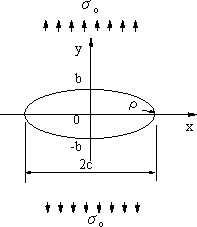 図6 楕円孔の場合 |
||||||||||||
| 応力集中係数αとおくと | ||||||||||||
| 曲率半径ρ→0の時、楕円孔が扁平になり、α→∞になることがわかる。つまり、脆性材料の場合はき裂のようになると応力集中係数αは∞大になり、大きくなり危険であるが、延性材料の金属の場合は降伏して降伏応力程度となる。 | ||||||||||||
| ■き裂による応力分布と応力拡大係数 各モードにおけるき裂先端の応力分布は次のように求められている。モードⅠの引張形式の場合は次式のようにもとめられている1),2)。 |
||||||||||||
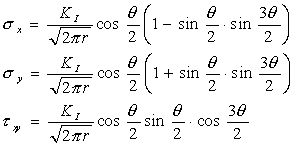 (5) (5)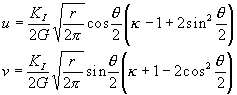 (6) (6)u,vはそれぞれ、変位のx,y成分  図7 座標軸 |
||||||||||||
| ここに、 G:剛性率 ν:ポアソン比 |
||||||||||||
| τxy の添え字の意味は,最初のxは,「x軸と垂直な断面における」との意味で,考えている断面を表し、次のyは,「y方向の」との意味で、方向を表している。 KI は | ||||||||||||
| で、応力拡大係数(stress intensity facter)と定義している。曲率半径が有限な円孔や楕円孔の場合は応力の集中度合いを応力集中係数αで表現したが,これに対応している。KI はモードⅠに対する応力拡大係数であることを示している。モードⅡ、Ⅲに対する応力拡大係数は次式で与えられる。応力拡大係数の補足 | ||||||||||||
| 一般的には、 | ||||||||||||
| で表され、αは試験片の形状、大きさやき裂形状、負荷応力の形式によって決まる無次元量である。 モードⅡのせん断形式の場合は次式のようにもとめられている。 |
||||||||||||
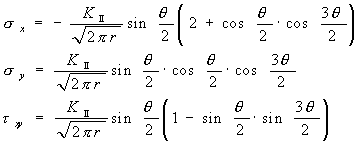 (11) (11)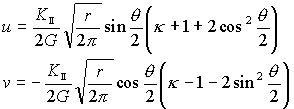 (12) (12) |
||||||||||||
| モードⅢの面外せん断形式の場合は次式のようにもとめられている。 | ||||||||||||
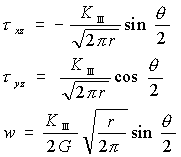 (13) (13) |
||||||||||||
| 3.切欠やき裂先端近傍の塑性変形5) |
||||||||||||
| モードⅠ 引張形式の場合、き裂先端の塑性変形を考える。変形状態の相違は、塑性変形長さsと板厚tの比で決まると言われている。 s < t の時は平面ひずみ状態、s > t の時は平面応力状態である。 |
||||||||||||
|
||||||||||||
| 4.破壊力学 モードⅠの引張形式の場合は次式のようにもとめられた。 |
||||||||||||
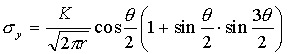 |
||||||||||||
| グリフィスの破壊応力(「材料の強度と破壊」の「脆性破壊」のページを参照)を求めるとき、弾性体において、き裂がcからc+dcまで増すときのエネルギー条件は、外力の変化がないとき、弾性ひずみエネルギーの減少dUが表面エネルギーの増加dWをまかなうときにき裂が成長を始める、つまり不安定成長の条件である。 |
||||||||||||
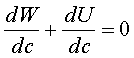 (15) (15) |
||||||||||||
| 表面エネルギーWと弾性ひずみエネルギーUは次式で与えられるので上式に代入して | ||||||||||||
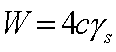 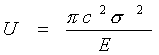 (16) (16)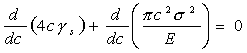 (17) (17) |
||||||||||||
| となる。整理して次式を得る。 | ||||||||||||
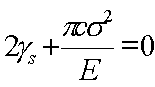 (18) (18) |
||||||||||||
| グリフィスの破壊応力は | ||||||||||||
| となり、σc に対応する応力拡大係数Kcとおく。 |
||||||||||||
不安定成長の条件での応力拡大係数を限界値考え、Kcを破壊靱性(fracture toughness)という。応力拡大係数がKc以上になったときき裂は成長する。Irwin4)らはき裂進展力(crack extension force)G=K2/E (平面応力)とおき、Gが限界値Gcに等しくなったときき裂の伝播が起こるとした。 |
||||||||||||
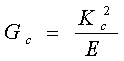 |
||||||||||||
| Gcは、靱性(toughness)あるいはき裂抵抗力(crack-resistance force)と言われる。この式は,表面エネルギー2γs(新しい面ができるために費やされるエネルギー)の代わりに,2γs+2γpを用いることで、き裂先端の小規模な塑性変形を伴う場合も成り立つとしている。 γp は塑性変形仕事(塑性変形のために消費されるエネルギー)である。 |
||||||||||||
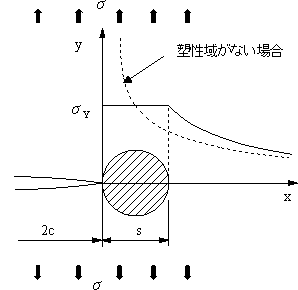 図10 き裂先端に小規模降伏が生じた場合の応力分布 |
||||||||||||
| モードⅠの平面応力状態の場合,き裂近傍の応力分布は式(5)であたえられるが,外応力σが大きくなり,き裂先端の応力が降伏応力σYに達し,塑性変形が生ずる。x軸上,y方向の応力分布は図10のようになる。塑性変形域の大きさをsとすると,小規模降伏,s<<cのとき近似的に | ||||||||||||
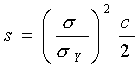 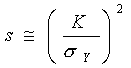 (22) (22)σY 降伏応力 |
||||||||||||
| と求められている3),6)。 き裂先端の開口変位φ(Crack Opening Displacement, COD)は,小規模降伏,s<<cのとき |
||||||||||||
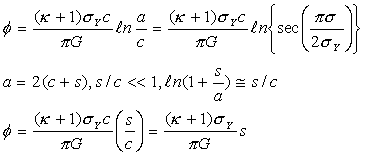 (23) (23)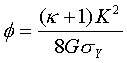 (24) (24) |
||||||||||||
| と求められている7)。 CODの値は、き裂が成長するための限界値として用いられている。つまり、き裂先端での変位がCOD値に達したときき裂が成長するという条件である。脆性破壊の項で述べたように材料は温度等の環境によって性質を変わるし、材料の組織や負荷速度等によって強さは変化するので、COD値の中にこれらのパラメータが入っていないので、CODを破壊条件とすることに疑問視する研究者もいる。 |
||||||||||||
| 式を導く過程などの詳細は文献9)をご覧下さい。 |
||||||||||||
| ■応力拡大係数(Stress intensity factor)の補足 | ||||||||||||
| 無限平板中にある長さ2c、曲率半径ρの弾性き裂(図11)のP(r,θ)における応力は式(26)のように求められている10)。ただし、c>>r>>ρの条件で求められている。弾性き裂端では、この条件では数学的に不連続点になるので、r→0ではσ→∞なる。式では、1/(r1/2) の項に入ってくる。 弾性き裂の曲率半径ρが有限の場合は最大応力の値σmaxは、応力集中係数Kαとして σmax=Kασ (25) として表すことができる。 |
||||||||||||
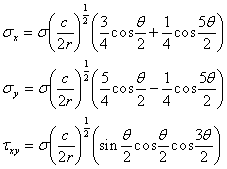 (26) (26) |
||||||||||||
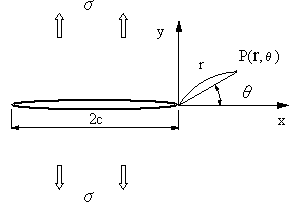 図11 |
||||||||||||
| ρ≒0の場合は、r→0ではσ→∞のため、応力集中係数では最大応力は表現できない。式(26)を見ると、弾性き裂近傍の局部応力は、外応力σとき裂長さ2cの平方根の積に依存することが明らかである。このことをIrwinは指摘し、これを示すために | ||||||||||||
| |
||||||||||||
| なる量、応力拡大係数(Stress intensity factor)が導入された。 式(26)は応力拡大係数を使うと次のように表現できる。 |
||||||||||||
| 有限寸法の板、形状に存在するき裂の場合に、応力拡大係数は と表すことが出来る。αは試験片とき裂の形状に依存する係数である。 |
||||||||||||
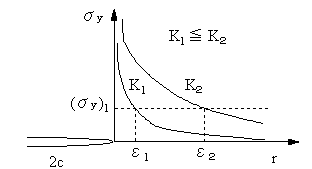
| 図12は応力拡大係数K1, K2の場合のき裂先端局部領域における応力σyのθ=0の応力分布状態を図示したもので、両者ともr→0ではσ→∞なります。同じ位置rではσyは応力拡大係数が大きいほど大きくなります。この傾向は応力集中係数と同様です。一定値(σy )1 以上の応力が生ずる範囲も応力拡大係数が大きいほど広くなります。 |
||||||||||||
図12 応力拡大係数K1, K2の場合のき裂先端局部領域における応力分布 |
||||||||||||
| 参考文献 1) M.L.Williams, J.Appl. Mech. 24(1957)109. 2) G.R.Irwin, Handbuch der Physik, Springer 6.(1958)551. 3) G.I.Barrenblatt, Advance in Appl. Mech.7(1962)55. 4) G.R.Irwin, Encyclopedia of Physics, Vol.Ⅵ, Springer, Heidlberg(1958). 5) G.T.Hahn and A.R.Rosenfield, Acta Meta. 13(1965)293. 6) D. S. Dugdale, J. Mech. Phys. Solid 8(1960). 7) J. N. Goodier and F. A. Field, Fracture of Solids, Roy. Soc. (1963)103. 8) J. R. Rice, Int. J. Frac. Mech. 2(1966). 9) 横堀武夫、材料強度学、岩波全書. 10) I. N. Sneddom, Proc. Roy, , A187, 229(1946). |