|
降伏は、せん断応力により、原子の結合が切れ、すべりが生ずるのであるから、局部的なせん断破壊である。設計時の強度計算の際、変形したら部品の精度が保たれない場合は、材料の強度として、引張強さの代わりに、降伏応力を採用するのであるが、この意味はこの辺にも理由がある。実際の設計では安全係数を考慮するので、発生する応力は降伏応力に達することはない。
|
| 3.1 |
炭素鋼における降伏点の特徴 |
|
鉄および軟鋼などにおける炭素鋼の降伏点は次の特徴的性質をもつ。
| (1) |
ある応力(上降伏点ないし降伏開始点)で塑性変形(すべり変形)が急激におこり,その応力またはそれより小さな応力(下降伏点)で塑性変形が進んでゆく。A点に
おいて、試験片R部の応力集中箇所から45°方向に最初のすべりが生ずる。 |
|
|
|
|
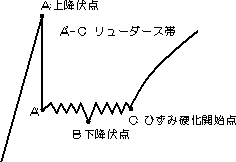 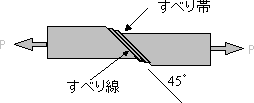
図3.1 降伏現象 図3.2 すべり変形
|
|
| (2) |
図3.1で、C点を超える伸びを受け塑性変形した試験片に,荷重除去後ただちに再荷重すると降伏点は表われない。
|
| (3) |
降伏点を越えて塑性変形を受けた試験片を荷重除去後、時間をおくか、低温焼鈍させた後、再荷重すると再び降伏点を示す。これをひずみ時効(strainageing)という。材料を強化する方法の一つである。図3.3(a)と(b)を比較すると降伏応力が上昇し、強度が上がっている。しかし、伸びは減少する。ひずみ
時効の後に表われる降伏点に対して,塑性変形を与えていない処女試片に最初に応力を加えたときに表れる降伏を初期降伏(initial yielding)という。
徐荷後、試験片を取り外し、再度取り付けて引張試験を実施した場合には、図3.3(c)に示すように、赤い線のような応力−ひずみ曲線になる。焼鈍するか時間をおいて引張試験を行えば、降伏現象が現れる。いずれも、図3.3(a)の応力−ひずみ曲線と比較すると加工によって強度が上がっていることが解る。伸びは減少する。
|
|
|
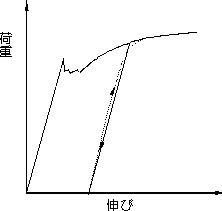 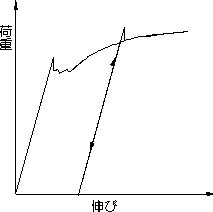
(a) 徐荷後、直ちに再負荷 (b) 徐荷後焼鈍、再負荷
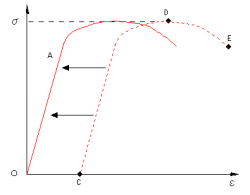
(c) 徐荷後、試験片を取り外し、再度取り付けて引張試験を実施した場合
あるいは、伸びを0に調整して再度負荷をした場合に
赤い線で示した応力−ひずみ曲線となる
図3.3
|
|
| (4) |
降伏点に達すると,Luders帯(すべり線の集合体)が表われ,下降伏点においてこれが進行する。この進行は図3.1の水平部分(A'-C)に相当するほとんど一定応力(下降伏応力)にておこなわれ,試験片平行部全表面にLuders帯がひろがった後、はじめて,その帯内の歪がおこり,そのとき応力−ひずみ曲線はひずみ硬化(Strain hardening)によつて上向きの形をとりはじめる(図3.1 C点以降)。A'C間の凹凸は、局部的な降伏(転位のクギ付け作用からの脱出)や局部的すべりの発生によるものと思われる。
|
| (5) |
上述の降伏現象および歪時効は炭素または窒素を含む場合にのみ表われる。多結晶 鉄の降伏では,炭素または窒素を含む場合に表われることが明かにされ,単結晶鉄の降伏については,炭素を含む場合に表われることが示されている。
|
| (6) |
鉄鋼以外の他の金属でも固溶体にある不純物元素ないし添加元素を含むときに降伏点が表われる。これは(5)と同様に,多くの研究によつてわかつてきたことである。
|
|
|
|
| 3.2 |
降伏現象のメカニズム------ コットレルの転位のくぎ付けからの解放
|
|
| (1) |
コットレル雰囲気---- 炭素鋼が粘り強い理由
転位線の真下の中心は原子面が抜けたため、結晶の格子がゆがんだ状態にあり、エネルギーの不安定な状態(転位が容易に移動できる原因)であり、この箇所に,CやNのような小さな溶質原子が侵入しやすい状況にある(コットレル雰囲気),転位の真下の引き伸ばされた原子間に、CやNのような小さな溶質原子が入り込み、転位のポテンシャルエネルギーを下げる(格子のゆがみを解消させる方向)。結果として、転位は移動しにくくなる(コットレルの転位のクギ付け作用)。材料は強化される。
|
|
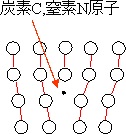
図3.4 転位のクギ付け作用
|
| (2) |
コットレルの転位のクギ付け作用からの脱出 上降伏点 Upper Yield Point
転位は移動しにくくなり、材料は強くなるが、この強度の値にも限界があり、ある応力(上降伏応力)で、クギ付け作用から一気に解放される。いったん解放されると、転位の移動により、転位の増殖→転位の集積→応力集中→他の箇所でのクギ付け作用からの解放が繰り返され、転位は、本来の低いせん断応力(下降伏応力)で容易に移動できるようになる。試験片全体にすべりが広がる。
|
|
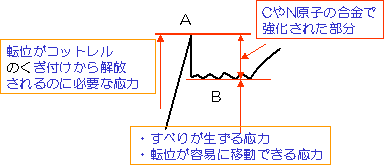
図3.5 降伏現象における各部の応力の意味
|
| (3) |
ひずみ時効の現象 Strain aging
降伏点をこえて塑性変形を受けた試験片に,荷重除去後ただちに再荷重した場合は、降伏点は表われない。荷重除去後、時間をおくか、低温焼鈍させた後、再荷重すると再び降伏点を示す。このことは、コットレルの転位のクギ付け作用から解放された転位の箇所に、再び、熱エネルギーを得てCやNのような小さな溶質原子が侵入し、転位をクギ付けし、材料は一層強化される。ひずみ時効は材料の強化法の一つである。 |
|
|
|
| 3.3 |
降伏現象の依存性
|
|
| (1) |
温度依存性
降伏開始点は常温以下においてとくに著しい温度敏感性を示すことが多くの実験で明かにされている(図
3.6)。温度の効き方が激しく、たとえば液体空気温度(−192℃)では常温の約4倍である。 |
|
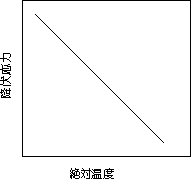 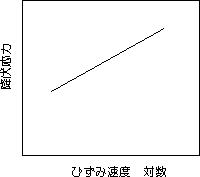
図3.6 温度依存性 図3.7 ひずみ速度依存性
|
| (2) |
ひずみ速度依存性
上,下降点(以下とくにことわらないときは降伏開始点ないし上降伏点を降伏点と呼ぶことにする)はまた荷重速度ないしひずみ速度に著しく依存し,速度の増加とともに増していくことが多数の研究者によつて詳細にしらべられている(図3.7)。 |
| (3) |
降伏遅れ
静的降伏点,すなわち,いわゆる普通の引張り試験で観察される降伏点よりもわずかに低い一定の応力を加えておくと,数秒ないし数時間後に突然降伏がおごることが観察される。また,ClarkおよびWoodたちは,静的降伏点以上の一定応力を急に負荷してから降伏開始までの時間おくれを測定し,著しい降伏点を示す鉄鋼にかぎつておくれ時間が存在することおよび
その時間が加えた応力および温度によつて著しく異なることを見出している(図3.8)。 |
|
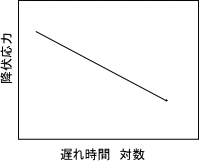
図3.8 降伏遅れ
|
| (4) |
フェライト結晶粒大きさの影響
下降伏点に対しては,組織的なものとして常温におけるHallたちの実験結果(式(1))、液体窒素温度におけるPetchの実験があり,これから下降伏点σy は、実験的にフェライト結晶粒平均直径dに対して、次式にて表わされる。この式を、Hall-Petchの式と呼び、金属組織と機械的性質との関係を表す重要な式である。
Hallたちの実験では,σoは単結晶の降伏点に大体等しい。大部分フェライト組織のものでは炭素含有量に無関係に結晶粒の大きさだけによつて決まってくる。
|
|
Hall-Petchの式
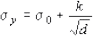
σy : 下降伏応力,σo : 単結晶の下降伏応力, d→∞の時、σy→σo
k : 材料定数, d : フェライト結晶粒平均直径
|
|
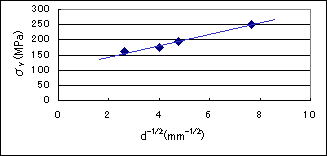
図3.9 結晶粒大きさの影響、常温 0.15%C炭素鋼
σy= 90.0 + 21.6d-1/2 文献
|
|
|
|
|
 
(a) 低炭素鋼の組織 (b)パーライトの拡大写真
図3.10 0.15%C炭素鋼の顕微鏡組織
|
| 3.4 |
金属を強化する基本的な2つの考え方
|
|
| (1) |
転位のような欠陥を完全になくす
金属中に存在する転位のような欠陥を完全になくすと理想的な強度になるが、現実的には困難である。しかし、実際の材料では、転位は1〜10μmに1個存在する程度であるので、材料を1〜10μm程度に細くすると転位が入らない確率が高くなり,理論的な材料の強さに近づく可能性がある。ウイスカー(whisker)、"ひげ結晶"が作られ、理論強度に近いことが分かったが、数mm程度の長さで実用的な研究がなされている。これに近いものとして、ボロンなどの金属繊維、炭素繊維,ガラス繊維(直径は10μm程度)などあり、ガラス繊維の引張強さ
3400 MPa ( 炭素鋼 400MPa)程度あり、複合材などに実用化されている。
|
| (2) |
転位を動きにくくする方法
転位は小さな力で移動し、増殖するのであるから、転位を動きにくくする方法として、合金や加工硬化等の方法が実用化されている。
|
| ◆ |
母体の金属原子と大きさが異なる原子を合金
結晶格子のゆがみが生じ、転位の移動の際大きなエネルギーが必要であり、転位の移動に対する抵抗となり,結果として強化される
|
|
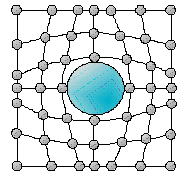
図3.11 合金による格子の変形
|
| ◆ |
コットレルの転位のくぎ付け理論
転位の周辺はエネルギーの不安定な状態(コットレル雰囲気)が転位が容易に移動できる原因となっている。この箇所に,CやNのような小さな溶質原子が侵入し,エネルギーを下げる。結果として、転位が動きにくくなる.つまり、金属が強化される(コットレルのくぎ付け作用)。
|
| ◆ |
異種金属同士の合金
異種原子間同士の結合は強く、結合を切るためのエネルギー大であり、転位が移動しにくくなる
|
|
| 3.5 |
点欠陥による強化
|
|
| ◆ |
転位の移動に対する障害物 点欠陥及びその集合
温度が高くなると欠陥は指数関数的に増加することを応用する。純金属を高温から急冷すると焼き入れされたことになり、相変化の過程で原子が移動するとき、その途中で点欠陥が生成される。完全な相変化が完了せず、多くの欠陥が閉じこめられる。冷却速度が大きいほど閉じこめられる欠陥の数は多い。転位が分散している空孔を通るときに転位線に食い違いを生じ、これが多数あると転位は運動に大きな抵抗を受ける。 |
|
|
|
| 3.6 |
加工による強化 -----加工硬化、ひずみ硬化
|
|
転位密度ρと塑性変形に必要な応力σの関係は次式のように求められている |
|
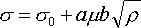 (2) (2) |
|
| (1) |
第1段階
容易すべり範囲,都合の良いすべり面上を転位が最初にを移動する。転位の増殖の開始
|
| (2) |
第2段階
他の応力の小さかったすべり面の転位も移動開始し、転位同士の交差,もつれ,転位の集積が生じ、それらが障害物となり、障害物が極端に多くなる。加工硬化が激しくなる。
|
|
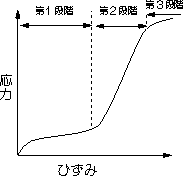
図3.12単結晶の応力ーひずみ曲線
|
| (3) |
第3段階
転位が別のすべり面に逃げる交差すべりが発生する。 |
|
金属を変形させ(加工)、転位密度を高くすると転位同士の交差,もつれ,転位の集積が生じ、それらが障害物となり、障害物が極端に多くなる。転位を移動させるには大きなせん断力が必要となり、結果として強化される。
|
|
| 3.7 |
結晶粒微細化による強化
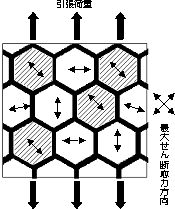
前節の説明のように,すべりが生ずる結晶面が決まっている。各々の結晶粒のすべり面と方向は異なる。これらが転位の移動に対して抵抗となる。材料力学の知識から、引張荷重を受けるときは、せん断応力の最大値は引張荷重に対して45゚の面に生ずる。せん断応力の最大値が転位の移動に必要なせん断力を超え、この面と結晶粒のすべり面が等しい結晶粒からすべりが開始する。図では矢印ですべり面を示した。ハッチングをした結晶粒からすべりが開始する。
|
|
 |
 |
 |
(a)最大せん断応力と一致した
すべり面からすべり開始 |
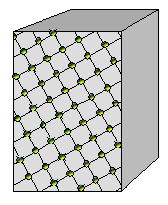
(b)単結晶 |
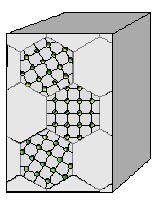
(c)多結晶 |
図3.13 微細化するほどすべりに対する抵抗となる結晶が増大する。
|
|
図3.2では単結晶の場合は比較的すべりは単純に表現できるが多結晶では各結晶粒のすべり面は異なるので実際は複雑なすべりとなる。
結晶粒を小さくするとすべりに対して抵抗となる箇所(すべり面が異なる)が増加し,結果として強度が上昇する。また,結晶粒が小さいと、結晶内のすべり線の長さが短くなり、集積する転位の個数が少なく,集積による応力集中が小さくなる(2.8参照)。
ホール・ペッチの実験式 |
|
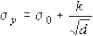 |
|
は、結晶粒が小さいほど降伏応力は高くなることを示している。 |
■ |
純鉄の結晶の変形と再結晶
純鉄に0.5〜2.2程度の塑性ひずみを引張試験機で与えた場合に図3.14のように結晶が変形する。変形前のフェライト結晶粒の平均粒径は60μmに熱処理により調整した。 |
|
小 ← 変形 → 大
図3.14 純鉄の塑性変形の様相 荷重は水平方向
|
|
 |
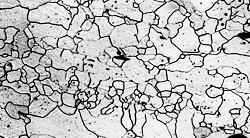 |
| (a) 熱処理前 破面近傍 |
(b) 650℃で3時間保持の熱処理 |
図3.15 再結晶現象を利用した細粒化
|
|
図3.15(a)は図3.14と同じ純鉄に大きな塑性変形を与えた後の写真である。その後、電気炉で650℃で3時間保持の熱処理をした場合、図3.15(b)のように再結晶により小さな結晶粒となり材料は強化される。
温度を上げると加工によって、格子欠陥、転位などの形で結晶内部に蓄えられたひずみエネルギーが解放され、転位が消滅してゆく(回復)。つまり、内部ひずみの少ない亜結晶が転位密度の高い部分を吸収して成長し、ひずみの少ない結晶粒に成長する。これを再結晶現象という。熱処理前の加工が大きいほど小さな再結晶粒が形成される。
材料の強度試験を行うとき、母材から切り出し、加工した試験片は旋盤や研削盤などの加工により、表面近傍は強度に変形を受けた状態にある。この影響を避けるため、試験前に必ず試験片のひずみ取り熱処理(焼鈍)を行う。この回復、再結晶現象を利用している。 |