| 以下の解説は、大学、大学院時代の師である元東北大学教授横堀武夫先生から学んだ知識です。更に詳細な内容については下記の参考文献を参照してください。 (1) 横堀武夫,「材料強度学」、技報堂(1955). (2) 横堀武夫,「材料強度学」、岩波書店(1974). |
|
| 2.1 | 金属の変形 荷重−伸び曲線 |
| 引張試験(tensile test)では、試験片を時間的に一定な割合(例えば,10mm/min)で引き伸ばし,伸びとその伸びを試験片に引き起こすのに必要な荷重(材料の抵抗力)を試験片が破断するまで連続的に測定し,記録します。このようにして得られるのが荷重ー伸び曲線です。図2.1に引張試験機の概要を示します。図2.2には低炭素鋼(炭素0.18%程度と鉄の合金,構造用鋼)の荷重ー伸び曲線を示します。 OからA’までは直線であり,荷重と伸びはフックの法則に従い,比例します。たいていの材料は,伸びが小さい場合はフックの法則に従う部分を有します。A’は直線の限界点で比例限度(proportional limit)です。A’からAまでは曲線となりますが、A点の荷重値より小さい値から除荷した場合は、もとの長さにもどります。A’点とA点の位置はほとんど差がなく、計測器の精度に影響されます。A点に達すると荷重は急激に減少し,Cまでは,荷重の多少の増減はあるが,ほぼ一定の大きさの荷重(ほぼ同じ大きさの抵抗力のもとで)で伸びだけが進行する現象を示します。 *国際的にはA'は、0.001%の永久ひずみを生ずる引張応力の値と定義されている。 |
|
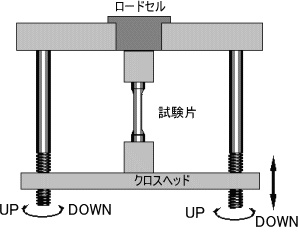 図2.1 引張試験機 |
|
| このAーCの現象を降伏(yielding)と言い、低炭素鋼の特徴です。A点を上降伏点(upper yield point),比較的平らな部分の中で一番荷重の低いB点を下降伏点(lower yield point)と言う。A点はすべり(slip)の開始点であり,試験片のR部から,すべりが発生し,その結果,C点にいたるまで帯状の筋(リューダース帯、すべり線の集合体)が試験片全体に広がることを示しています(図2.4)。一般に形状が変化する部分では、応力集中(後に解説)のため、形状が一様な箇所より応力が高くなるので,すべりはここから発生し,すべりの方向はほぼ最大せん断応力方向(荷重軸方向とは45゚をなす)です。低炭素鋼は多結晶であるので、実際の現象は図よりも複雑です。 OAは弾性変形で力を取り除くと元の長さに戻る変形をしており、A点以降は塑性変形で力を取り除いても元の長さに戻らず,永久のびが残る変形です。ほとんどの材料は,変形が小さいうちは,弾性変形,大きくなると塑性変形を示します。ガラス,セラミックスなどは弾性変形のみで,比較的もろい材料です。 |
|
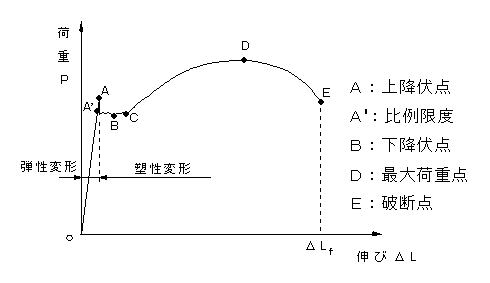 図2.2(a) 引張試験で得られる炭素鋼の荷重−伸び曲線 |
|
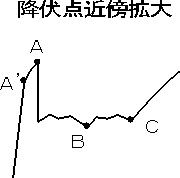 AA'は曲線であり、フックの法則に従わないが、荷重を徐荷した場合に永久ひずみは残らない |
|
| 2.2 | 応力−ひずみ曲線 |
| 荷重−伸び曲線を、荷重を変形前の試験片の断面積で割り、応力で表し、伸びを試験片平行部の長さで割り、ひずみに変換して書き直したもの応力−ひずみ曲線といいます。 この図から、材料の強さに関する情報が得られます。材料の種類によって曲線の形状が異なります。 |
|
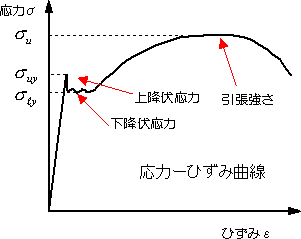 図2.2(b) 低炭素鋼の応力−ひずみ曲線 |
|
| ■ | 明確な降伏点を示さない場合 明確な降伏点を示す材料は炭素または窒素を含む場合にのみ表われる。炭素鋼が代表的であるが、鉄鋼以外の他の金属でも固溶体にある不純物元素ないし添加元素を含むときに降伏点が表われる。銅、アルミのような材料は降伏現象を示さない。 耐力は降伏現象を示さない材料の大きな塑性変形を生ずる前の応力(降伏応力に相当と解釈)を表し、0.2%の永久ひずみを生ずる時の応力の値で定義しています。永久ひずみですからすでに塑性変形はしています。降伏現象を示す材料は炭素鋼、窒素など含む金属などですが、これらの上降伏点もいろいろで、上降伏点のひずみは0.2%にはなりません。大きな塑性変形を生ずる前の応力と言うことで、降伏点のないすべての金属に適用する定義です。 図2.2(c) は降伏点を示さない材料の応力−ひずみ曲線です。0.2%のひずみがQ点で、ここから、フックの法則が成り立つOAに平行線を引き、応力−ひずみ曲線と交わる点をPとします。P点から横軸に平行線を引き、応力軸と交わる点の値が耐力σ0.2です。P点のひずみεは、OHで、弾性ひずみQHと塑性ひずみOH(永久ひずみ0.2%)の和になります。P点まで引張り、この点から伸びを0に戻すと、荷重−伸び曲線でP点に対応する点から、PQに沿ってAOと平行に下がり、荷重0の時はQ点に相当するところで止まります。OQが塑性変形によって生じた永久ひずみで、QHの値が元に戻った弾性ひずみの部分と言うことになります。P点のひずみは、元に戻る弾性ひずみと元に戻らない塑性ひずみの和であることです。 |
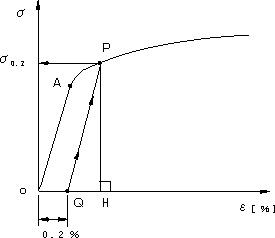 図2.2(c) 耐力σ0.2の求め方 |
|
| ■ | 塑性変形における応力とひずみ 図2.2(d)のP点は降伏後、塑性変形した点である。このP点における応力は、σP,ひずみはεtである。εtは全ひずみであり、弾性ひずみと塑性ひずみの和である。P点から徐荷すると、フックの法則が成り立つAOに平行に応力は下がり、PQ似沿って低下し、荷重0ではQ点に達します。 この時、QHに相当するひずみεeは、徐荷すると0になる弾性ひずみ、OQは元に戻らないひずみεp、塑性ひずみ、永久ひずみである。(弾性ひずみ+塑性ひずみ)がP点におけるひずみで、これを全ひずみεtと言う。εt =εe+εp εt :total strain ,εe:elastic strain, εp: plastic strain |
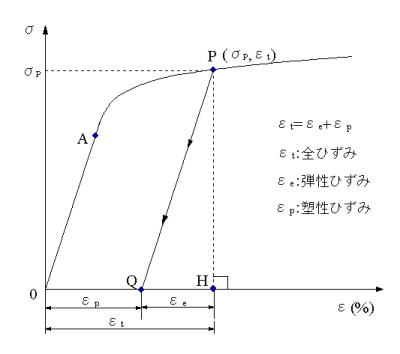 図2.2(d) P点から徐荷する場合 弾性ひずみと塑性ひずみ, AO//PQ |
|
| ■ | 材料による代表的な応力−ひずみ曲線の形状 |
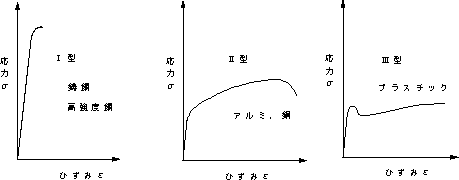 図2.3 材料によって異なる応力−ひずみ曲線の形状 |
|
| 塑性変形の現象は工業製品に応用されています。降伏以後の変形は負荷徐荷後、永久伸びが残るわけですから、鍛造,圧延,線引きなどの加工,変形させる塑性加工や変形させることで材料の強さが向上するひずみ硬化、時効硬化を材料の強化として利用しています。 |
|
| 2.3 | 変形機構としてのすべりと双晶 |
| 金属の変形の仕方はすべり(slip)と双晶(twin)以外にありません。この現象について述べます。 2.3.1 すべり(slip)による変形 カードが崩れるように,ずれることによって変形することをすべりと言います。この現象については後に詳しく述べますが、結晶のすべり面とすべり方向は決まっていて、他の面上や方向にはすべることができません。表1に示します。 |
|
 |
|
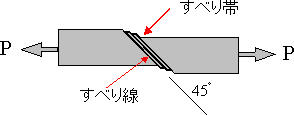 図2.4 すべり変形の模式図 |
|
| 2.3.2 双晶(twin)による変形 ある面を境にして,結晶格子が対称にずれる変形で図2.5に示します。双晶面と双晶方向も金属により決まっていて、これを表2.1に示します。波線の矢印のように原子が移動し、双晶面に対して、原子の並び方が対象になるように変形します。 |
|
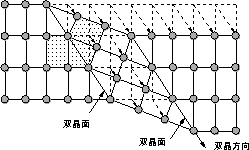 図2.5 双晶(twin)による 変形 |
|
表2.1 双晶が生ずる結晶面 |
|
| 2.4 | 格子欠陥 点状欠陥 結晶は原子が規則正しく並んでいると述べましたが、実用金属では並び方に乱れが多くあるのが一般的です。格子点の位置の原子が抜けたり(格子欠陥)、余分に入ったり(格子間原子)して乱れた箇所を点状欠陥といいます。アルミなどは1cm3 に室温では約8×1010個あると言われ、点欠陥は温度の上昇と共に増加します。 |
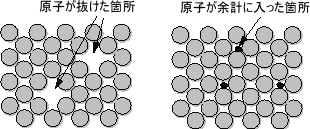 図2.6 点状欠陥 |
|
| 2.5 | 転位とその性質の概説 |
| 2.5.1 刃状転位 edge dislocation Taylerと Orowanが1934年に転位の理論を提案し,その後,転位の存在も電子顕微鏡などにより確認され,金属の変形や挙動の説明が飛躍的に発展しました。 図2.7のように、原子面が途中から抜けている面状欠陥を刃状転位(edge dislocation) と言います。不完全な原子面が刃物の刃のように見えるからです。破線より上では原子面が余計に詰まった状態で、圧縮状態であり、破線より下では原子面が抜けた状態で引張状態になっています。原子の乱れは、転位の中心で大きく、中心から離れるに従い、乱れは小さくなり、正常な本来の原子間隔に近づき、中心から5〜6原子間隔で乱れはなくなると言われている。転位は図の場合は正の転位で記号⊥で表し,破線の下側に余分な原子面が入った転位を負の転位,記号┯で表します。また,転位の中心を結んだ線を転位線(図2.7(b)のAB)と言います。 図2.7(a)の矢印の方向にせん断力が作用した場合は,破線の面上を転位は移動することになりますが,この面がすべりが可能である面(表2.1)であることが必要です。金属によって決まっているすべり面以外では後に述べるように移動できません。 |
|
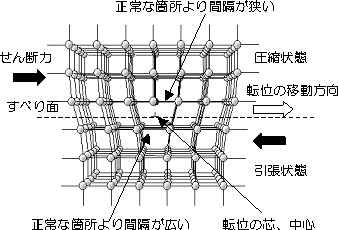 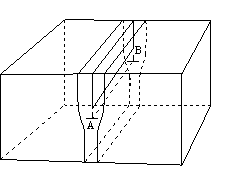 図2.7 刃状転位 |
|
| 2.5.2 らせん転位 screw dislocation 転位のもう一つ基本的なものにらせん転位があります。図2.8のようにABの線を中心に,1回転すると1原子面だけらせん階段のようにずれることからこの名前が付いています。ABが転位線で,左巻と右巻があります。図のように力が働いたとき移動方向は矢印に示すとおりで,力の方向は転位線と平行で,移動方向は垂直となります。 |
|
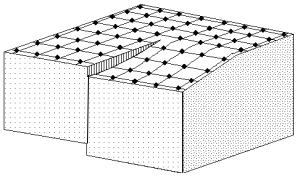 (a) |
|
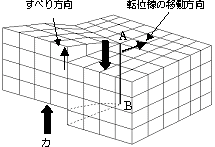 (b) 図2.8らせん転位 |
|
|
2.5.3 混合転位 らせん転位と刃状転位の混じり合った中間的な転位に混合転位があります。現実に存在する転位の形状です。 |
|
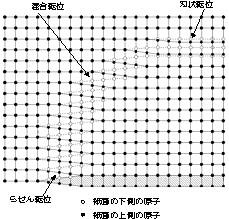 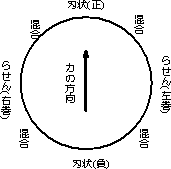 図2.9 混合転位 |
|
| 2.5.4 転位密度ρ dislocation density 実用金属には多くの転位が含まれています。転位の量を表す方法として,1cm3の結晶存在する転位線の長さの総計で表す転位密度ρ(cm/cm3)があります。cm/cm3は1/cm2となるので,この表現は,結晶1cm2 を貫く転位の個数と言うことになります。ひずみや転位を取り除くのに,再結晶現象を利用し,再結晶温度以上で一定の時間保持する焼鈍あるいは焼きなましという熱処理があります。よく焼きなました金属でさえも転位密度は106〜108 cm/cm3 程度あります。塑性加工した材料では 1010〜1012 cm/cm3 程度で, 1cm3当たり地球を25周するほどの長さの転位線に相当します。また,加工することにより転位は増えることを示しています。 よく焼きなました金属では,転位線の間隔は1〜10μm程度であり,3000〜5000原子に1個の転位が存在することになります。 2.5.5 結晶のすべり面とすべり方向 金属の結晶はせん断応力τにより図2.10のように変形し,限界を超えると原子の結合が切れ,ある面(破線)を境にしてずれが生じます。この現象をすべり(slip)といい,破線をすべり面と言います。 |
|
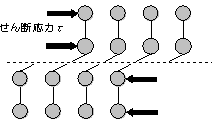 図2.10 結晶のせん断変形 |
|
| 金属によって,すべり方向とすべりの結晶面が決まっています。この面以外ではすべることはできません。原子が最も多く詰まっている面がすべり面となります。 |
|
表2.2 結晶のすべり方向とすべり面 |
|
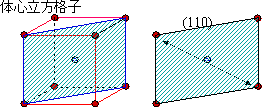 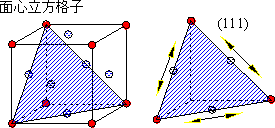 図2.11 すべり面とすべり方向 |
|
| 面心立方格子の場合、 (111)面に6個の原子,密に詰まって,隣の原子との距離小→移動の際、小さいエネルギーですみます。 |
|
| 2.5.6 転位などの欠陥がない、理想結晶のすべり変形 図2.12に転位などの欠陥が全くない場合のせん断応力τが作用し,破線を境界とする原子の結合が全部切れ,1原子間距離だけ移動した場合を考えます。 |
|
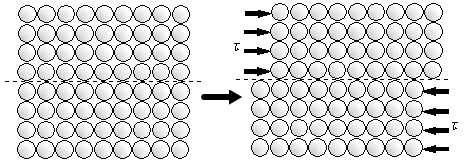 図2.12 欠陥,転位がないときのすべり変形 |
|
| 上下面の原子の結合が同時にいっぺんに切れ,隣の原子の位置に入り再び原子同士は強固に結合します。原子の数は天文学的な数字で、結合を切るためのエネルギーは大きく,莫大なエネルギーが必要となります。 2.5.7 刃状転位が存在する箇所にせん断力が作用する場合 図2.13で,転位の芯の近傍の原子A, Bの状態に着目しますと,破線より上方の原子は原子面が余計に入ったため,格子間隔が通常より狭くなっているので原子Aは元の格子間隔に戻ろうと矢印の力が働いています。一方,破線より下方の原子は,通常より格子間隔は引き伸ばされており,同様に元の格子間隔に戻ろうと原子Bには矢印の方向に力が作用している。このような状態にあるところにせん断応力が作用すると原子Aと原子Bの結合は切れやすく,しかも小さなせん断応力で切れる。結果的に,図2.14のようになり,転位が1格子間隔だけ右に移動したことになります。 |
|
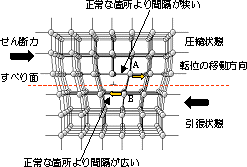 図2.13 転位が存在する場合のせん断変形 |
|
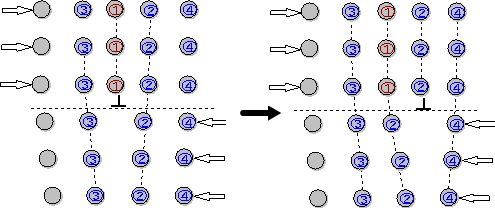 (a)移動前 (b) 移動後 図2.14 転位が1原子間距離だけ移動 |
|
| 転位の周りの応力(力)の分布状態から、かなり小さい力あるいは,エネルギーで移動できる。1原子間距離の移動を順次繰り返し,転位が結晶の端まで移動して抜ける.結果的に結晶全体が1原子間距離のすべりが生ずる. |
|
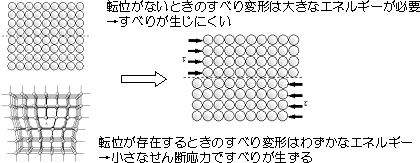 図2.15 転位の移動 |
|
| 2.5.8 転位が小さな力で容易に結晶の端から端まで移動できるのと似たようなこと ----- アナロジィ 転位がどうして小さな力で移動できるのか,解釈しにくいこともあり,いろいろな例を持ち出して説明されている。図2.16の絨毯の例では,重い絨毯の端を両手で持って引っ張り,距離Sだけ移動するのはかなりの力が必要(転位のない結晶のすべりに相当)ですが端をSだけ押してしわを作り,このしわを押して他端まで押してゆくと最終的に絨毯全体が距離Sだけ移動したことになる。絨毯を引っ張って移動させるよりも遙かに楽に移動できる。このしわが転位に相当する。 |
|
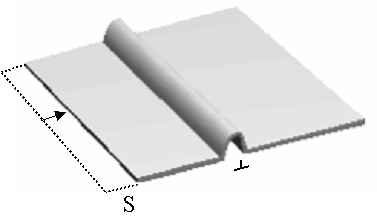 図2.16 絨毯の移動の場合 |
|
| 2.5.9 エネルギー論的説明 転位は何故小さな応力で移動できるのか 図は水素原子が近づいたときの場合であるが,原子1の電子と原子2の陽子,原子2の電子と原子1の陽子の間に働く引力,原子1の電子と原子2の電子,原子1の陽子と原子2の陽子の間に生ずる反発力。引力と反発力が釣り合って0となり,この時の原子間距離で安定する。ポテンシャルエネルギーは最小となる。 |
|
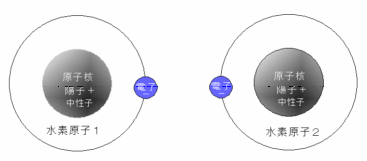 図2.17 |
|
| 結晶の格子間隔も同様であり,転位がない場合は図のようにエネルギーの谷間にあり,この状態の原子を全部移動するためには,各々がエネルギーの山を超える必要がある。転位が存在する場合は,図のように,力学的考察から転位の原子面はエネルギーが高く,どちらに移動しても良い状態にあり,少しの力で移動する。 | |
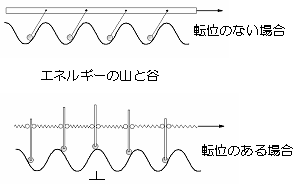 図2.18 エネルギー論的説明 |
|
| 2.6 欠陥のある材料と全くない理想的な材料の場合の強さの比較 ・理論的せん断強さ 原子の結合が切れる時に必要な単位面積当たりの力τ、xが大きくなるとやがて切れる。 ・せん断強さの実測値 現実に使用されている材料のすべり始めるときの強さ。xが大きくなるとやがて切れる |
|
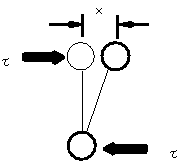 図2.19 せん断変形 |
|
表2.3 臨界せん断強さAと・実測値Bの比較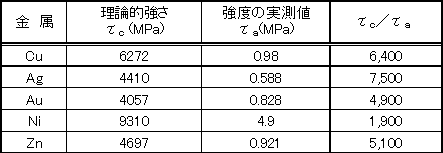 |
|
| ◆欠陥のない材料の 1/7500〜 1/1900の強さ 「 転位のような欠陥の存在がすべり強度を大幅に減少させる」 Taylerと Orowanが1934年,欠陥のない材料と実用材との強さの大幅な相違の説明のための理論として転位のモデルを提案し,その後,実験的に透過型電子顕微鏡により転位が観察された。以来、金属に関するいろいろな現象は,ほぼ転位で説明できるようになりました。図2.19においてABが転位線で,電子顕微鏡では 転位の中心がゆがんでいるため、転位線の近傍が黒い線となって観察される。 |
|
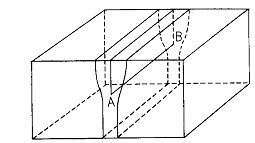 図2.19 ABは転位線 |
|
| 2.7 転位の主な性質 (1). 転位の周辺に応力場ができる 原子の配列の乱れが周辺に影響を及ぼし,ひずみ、応力が生じている。格子の乱れは,5〜6原子の範囲である。 (2).同符号同士は反発,異符号同士は引き合い,合体して消滅 |
|
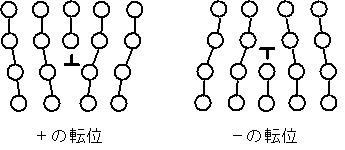 図2.20 正(+)の転移と負(−)の転位 |
|
| (3). 小さな力でも転位は増殖して莫大な量の転位が次々発生 ●フランクリードの機構 すべりの量は観察の結果,800〜1000個の転位が通過した量に相当するので、転位が増殖する仕組みが、フランクとリードによって提案された。 |
|
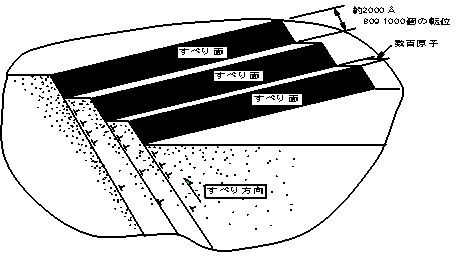 図2.21 すべり変形の大きさ |
|
| ■転位の増殖機構 (a).転位線ABはすべり面上,その他の転位線はすべり面以外で、移動不可。A,B点で固定されている。 (b),(c).そのため、せん断応力を受けるとAB部の転位は輪のように変形。さらに大きく なり、 (d).左巻,右巻のらせん転位が出会うと消滅し、 (e).独立したループが生成される。 (f).この過程が繰り返えされ、ループが次々生成され、多重ループとなる AB:フランクリード源と言う。多数の転位が発生する源。 |
|
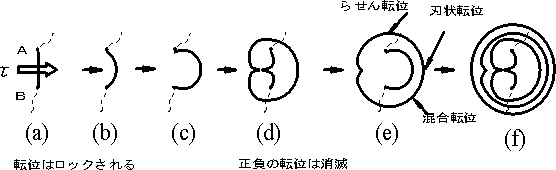 図2.22 転位の増殖機構 |
|
| 転位のループがSi単結晶の場合に透過型電子顕微鏡により観察され、この機構が認められた。 |
|
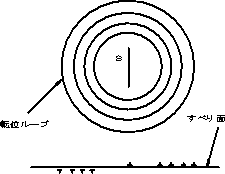 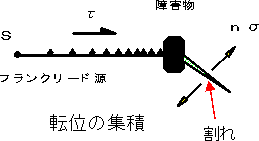 図2.23 転位ループとすべり面状の転位 図2.24 障害物による転位の集積 |
|
| 2.8 | 転位の集積 |
| 大量に発生した転位は,結晶境界,転位などの障害物により動きを止められ集積する。同じ符号の転位は反発するので、更に多くの転位を集積させるためには、せん断応力を大きくする必要がある。これが加工硬化(ひずみ硬化)の原因の一つとなっている。 この箇所に,局部的に大きな力が集中し,材料の強さを減少させる。低温脆性破壊などにおいては、図2.24の割れ(Crack)が破壊の起点となりうる。結晶粒径が大きいと、集積する長さ(範囲)が大きくなり、集積する転位も多くなり、結果として応力集中が大となり、強度を低下させる(降伏応力、破壊応力の結晶粒大きさの依存性にも関係)。 障害物は、結晶境界の他、転位同士、介在物などである。 |
|
| 2.9 | 欠陥のない結晶(理想固体)の強さの計算 |
| ■2つの原子間に働くポテンシャルエネルギーUと力F 図2.17で説明のように,2つの原子間に働くポテンシャルエネルギーUと力Fは量子力学や化学の分野等で次のように求められている。図2.25は2つの原子間に働く相互作用力Fについて示した。引力と斥力が釣り合うところ(合力F=0)が原子間隔となる。外力を加えて原子を引き離すためには、合力Fに逆らって外力を作用させる必要があり、最大値を超える(図の理論的強さ)と結合は切れることになる。この部分の曲線をSin関数で近似して理論的強さを計算する。 |
|
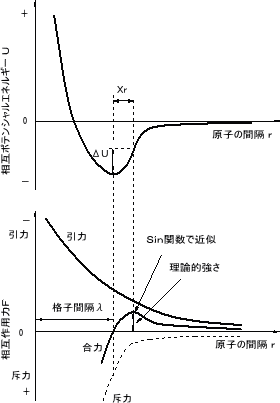 図2.25 2つの原子間に働く相互ポテンシャルエネルギーと相互作用力 |
|
| ■引張の場合 2つの原子をxだけ引き離すのに要する応力σは次式で近似され、最大値σcを越えたとき、原子間の結合が切れ、破壊が生ずる σ=σcsin(2πx/λ) σc:理論的引張強さ λ:格子間距離 近似式として次のように求められている。 σc≒ E/10 E:ヤング係数 |
|
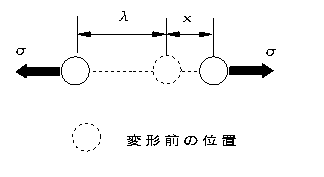 図2.26 引張の場合 |
|
| ■せん断の場合 外応力τが大きくなり、 最大値τcを越えたとき原子は隣の位置に移動.1原子間距離のすべりが生ずる。 τ=τcsin(2πx/λ) 近似式として次のように求められている。 τc≒G/2π τc:理論的せん断強さ、 G :剛性率,横弾性係数 |
|
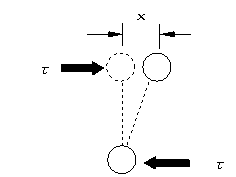 図2.27 せん断の場合 |
|
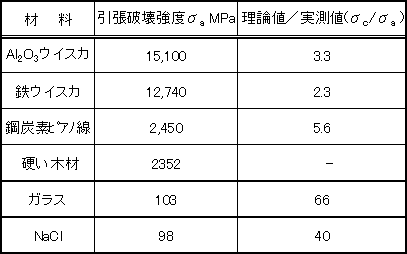
| ■理論計算値と実測値の大幅な相違 せん断強さτcの実測値は,理論値の1/100〜1/1,000になっている。この差は何から生ずるか? 理論計算では,結晶格子は理想的に完全な状態,格子欠陥などの欠陥がないことで話を進めてきた。実際は,格子欠陥,空孔や介在物による欠陥が多く含まれ,それらによる応力集中効果によって外荷重は小さくとも,材料の内部では大きな応力が生じ,σc,τcを軽く越えると言うことが起こるからである。種々の欠陥の中で,特に結晶格子の面状の欠陥である『転位(dislocation)』が材料の強度に大きな影響を及ぼす。 |
|
| 表2.4 引張強さの理論値σcと実測値σaの比較 | |
 |
|
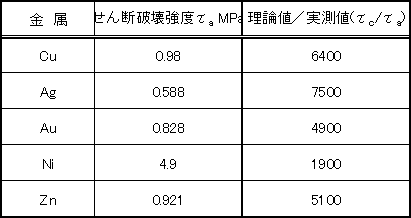
| 表2.5 せん断強さの理論値τcと実測値τaの比較 | |
 |
|
| *参考文献 転位について詳細に書かれている著書です 鈴木秀二、「転位論入門」、アグネ |