| ウッドホーンの原理と設計計算 |
||||||
| (1).ホーンスピーカーのの原理と構造について |
||||||
|
新井悠一著、「ホーンスピーカー設計・製作法」ではかなり詳細にホーンについて述べられています。また、ホーンの原理、設計法、計算方法、数種の設計例が書かれています。その中から、ウッドホーンを製作したとき準備した資料を紹介します。また、ホーン設計計算のプログラミング例も記載されていますが、現在は、Excel
のマクロ処理のVBAで簡単に作ることができます。
ホーンはスピーカーユニットに付けることにより効率が10数倍上がります。遠くにいる人を呼ぶときに、口に手を当ててホーンを作るのも、トランペットやサックスのホーンも同じ役割と言われています。
よく知られている「エクスポーネンシャルホーン」の場合、音の入り口から出口までの断面積が指数関数的に変化することを意味します。図1で、ホーン入り口、ホーンスロートの断面積Soとすると入り口からxの位置での断面積Sはエクスポーネンシャルホーンのとき、次のような式になります。
|
||||||
| m :フレアコンスタント fc : カットオフ周波数Hz
c : 音速 34,400 mm/sec
|
||||||
| 「ハイパーボリックホーン」の場合は |
||||||
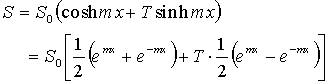 (2) (2)
となる。
|
||||||
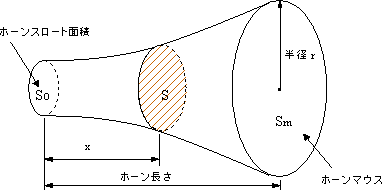 図1 ホーン形状と断面積 |
||||||
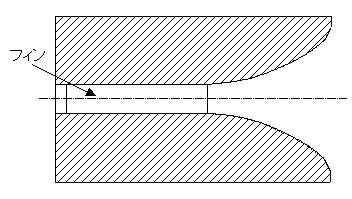
| フィンで音道を仕切るデフラクションホーンの場合、平面図と断面図は図2のようになります。 |
||||||
|
||||||
| ホーンマウス(ホーンの終端)での面積Smとすると、次式で与えられる。 |
||||||
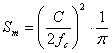 (4) (4)セルが5つであれば、 1つの ホーンセルのホーンマウス面積は、 Sm / 5 となる。C:音速34400cm/sec |
||||||
| ■ホーンの設計計算 |
||||||
|
ホーンの形状・寸法を決めるための計算は、位置xにおける(1), (2)式で与えられる面積Sを確保することにある。ホーンセル1つ当たりについて計算すればよいが、両側のホーンセルについては、フィンの長さlo以降は、ウッドホーン側板の形状をフィンの延長として変えることになる。フィンがある場合は、フィンの長さまでは、フィンの高さhoは一定である。その後は、フィンの形状の延長とウッドホーンの高さ方向の形状を変えることになる。
|
||||||
|
(1) 計算
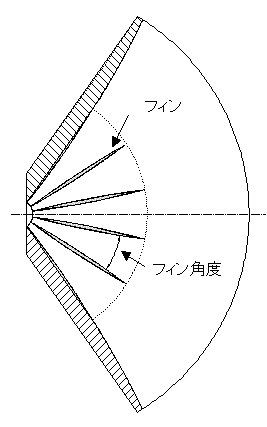
図3,4のように、フィン間の角度θ、スロートの高さho(フィンの高さ)、カットオフ周波数fcとおく。各フィンの中心線の延長が交わる点をOとして、この点をxy座標の原点に取る。半径Rの円周上に各フィンの端がある。このRを"フィンのならび半径"という。A,B点は2つのフィンの端点で、フィンのならび半径の円周上にある。ホーンセル数が5の時
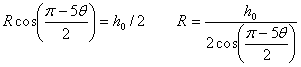 |
||||||
| xの位置での2つのフィン間隔をbと置く(図3)。S=bhoとなり、この面積が(1)式か(2)式に従うように、フィンの位置と厚さを計算により決定する。
点X(x,y)から、フインの中心線に垂直に線を引き、中心線との交点をX1(x1,y1)とする。従って、AとX1はフィンの中心線上にあり、AX1⊥XX1である。 x軸とフィンの中心線AX1の角度はθ/2、AX1の直線の式は、傾き−moとすると |
||||||
| |
||||||
| となる。図4で半径Rの円の式は | ||||||
| となるので、直線と円の交点A(xo,yo)とおくと、(5),(7)式から
|
||||||
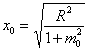 (8) (8) となる。 |
||||||
| ABの面積、ホーンスロート面積Soは | ||||||
| |
||||||
| ホーンの断面積Sは、各ホーンの場合に次式で与えられる。 |
||||||
| |
||||||
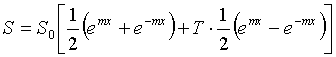 ハイパボリックホーン ハイパボリックホーン |
||||||
| 図4、5のように、入り口からxの位置での断面積S(エクスポーネンシャルホーン or ハイパボリックホーンの式)が確保出来るようにフィン形状・寸法( x<lo )とホーン形状( x>lo )を決定する。 0≦x≦lo の範囲では、フィンの高さhoは一定であるので、フィンの厚さを変えることでSを確保する。lo≦xでは、図3のようにホーンの形状dhを変えることでホーンの面積Sを確保する。 |
||||||
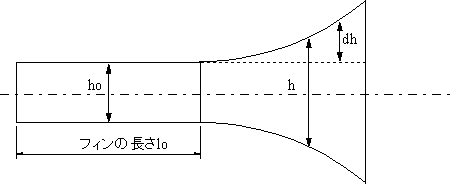 図3 断面図 |
||||||
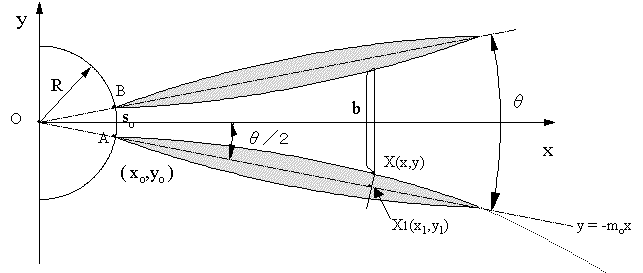 図4 平面図 |
||||||
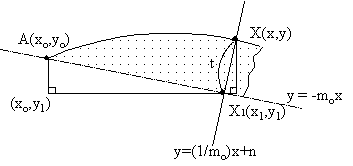 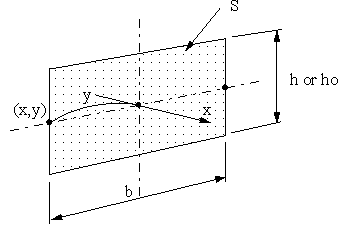 図5 フイン部の詳細とxにおけるホーンの面積S(=bh or =bho, b=2y ) |
||||||
| ●0≦x≦lo のとき |
||||||
|
ホーンの面積Sの式中の xには x'-X2 を代入し、x' をX2からホーン長さRmax+1程度まで変えてSを計算する。
x' =X2 の時、 S=S0とする。図4でAB部の面積 フィン縁上の点X(x,y) 、X点を通り AX1の直線と垂直に交わる直線の式は、交点をX1(x1,y1)とおくと
|
||||||
| |
||||||
|
点(x,y)が与えられれば、(12)式のようにnも決まります。moは(6)式で与えられます。
X(x,y)におけるフィンの板厚tを求める。(5)式と(11)式の交点X1の座標は
|
||||||
| |
||||||
|
となります。
フィンの厚み2t(2XX1)は
|
||||||
| |
||||||
| AX1=dとおくと | ||||||
| |
||||||
| ●側板の形状 lo<xのとき | ||||||
|
フィンの形状はdに対するフィンの厚さ2tを求めれば形状が決まる。フィンの厚さ2t=0になったときフィンは終わるが、その後はホーンの高さが曲線に対応することになる。幅方向はフィンの形状の延長として計算する。
|
||||||
| |
||||||
| 図5から、 b=|2y| の関係がある。表1にxとh、dhの値を示した。ホーン長さx≧cmの範囲の値である。 |
||||||
表1 Excelのマクロ処理で計算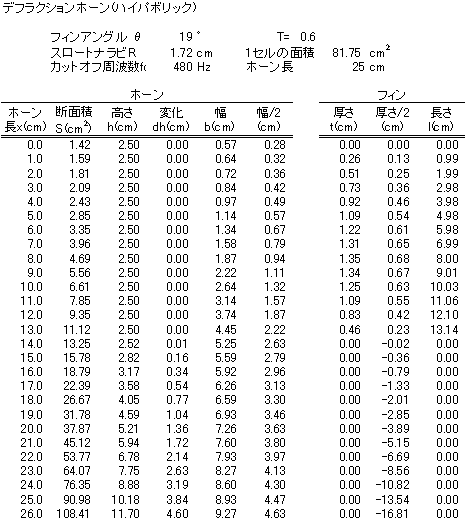 |
||||||
| ●側板の形状 lo<xのとき | ||||||
|
両側板の厚さ方向の曲線はフィン長さ以降のフィンの厚さ/2とホーン長さxの関係で決められる。
表2と図6、表3に示した。
|
||||||
| 表2 |
||||||
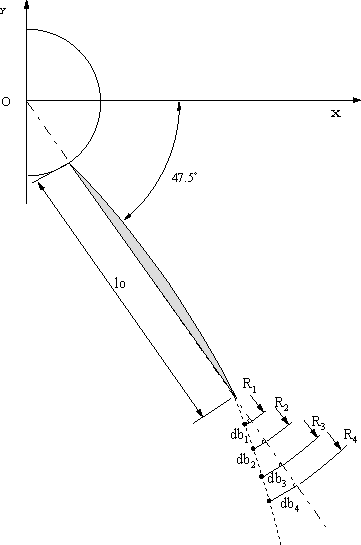 図6 側板の形状 |
||||||
| 表3 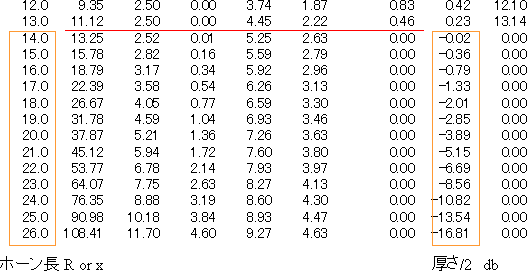 |
||||||
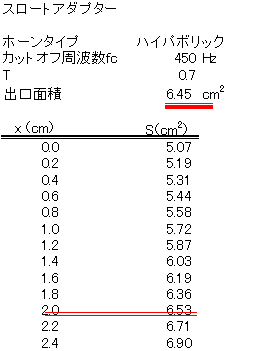
| ●アダプター板厚の計算 | ||||||
| ドライバーの音道の出口は1inか2inの円形、ウッドホーンの入り口は1inか2inのの正方形である。円形から正方形に変化するが、ホーンと同じように、Soを表のようにおいて、Sを0.1cm刻みで計算する。Ssに近い値を与えるxが板厚tなる。プログラムのSoを表のように置いて0.1cm刻みで断面積Sを求めると良い。 |
||||||
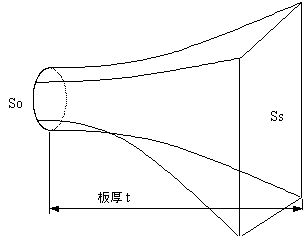 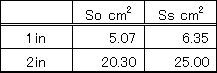 図7 |
||||||
|
||||||
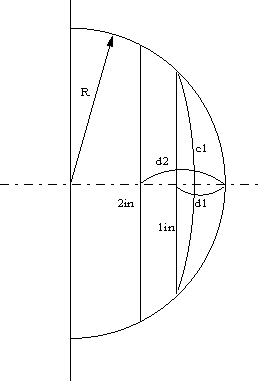
| ● ドライバー取り付けアダプターの寸法例 |
||||||
|
使用するドライバーにより、ドライジー取り付け穴の位置は異なる。また、ホーンへのアダプター取り付けはホーン寸法が決まってから決める。1 inホーンの一例を図に示す。ホーン側には、M4程度のネジの鬼目ナットを埋め込むと簡単である。
|
||||||
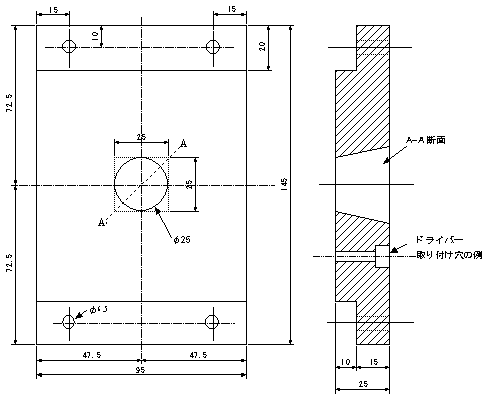 図8 表6の計算とは別な図面である。表6では板厚は20mmとなる。 表 7 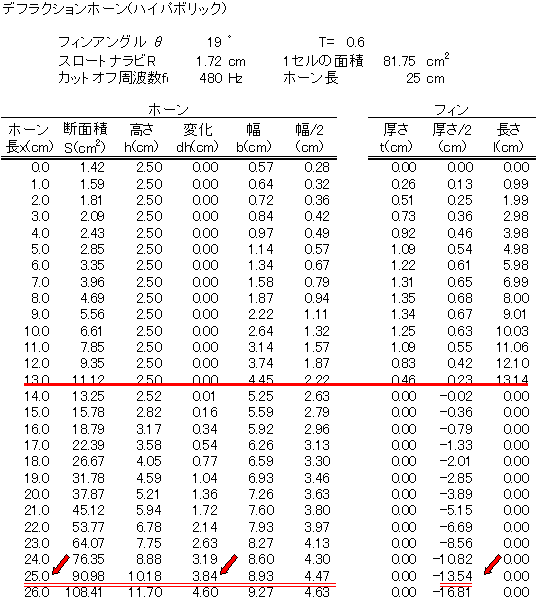 |
||||||
|
1セルの出口のホーン面積81.75cm2 (表7)はホーン長x=25cmで達成されるので、フイン開始点から250mmのホーン長になる。このとき、dh=
3.84 cm となり、ホーン部の厚さは50mmで良い。勿論、60mmでも良い。
|
||||||
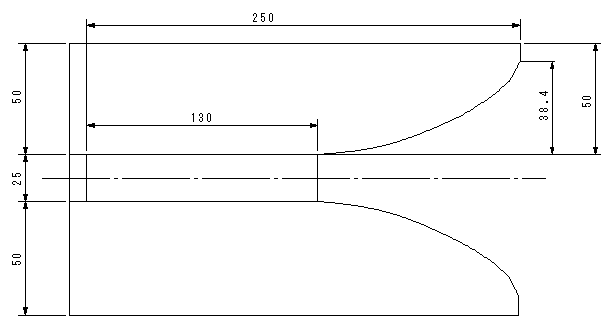 図9 寸法の単位はmm |
||||||
|
●スロート部の寸法計算 ----- 表7の場合
1inの場合、図10のように
|
||||||
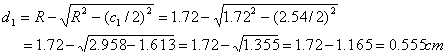 図11でホーンの長さは 250 + 5.6 =255.6mm |
||||||
|
||||||
| ●ホーンの側板の寸法 図11
表7から ホーン長x=25cmで 厚さ/2 = 13.54mm であるので側板の板厚t = 25 mmとする。
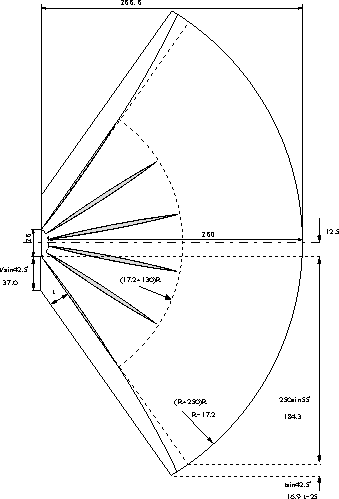
t/sin42.5゚= 37.0 mm tsin42.5゚= 16.5 mm 250sin47.5゚ = 184.3
ホーン幅 = (12.5 + 184.3 + 16.9 ) ×2 = 427.4 mm |
||||||
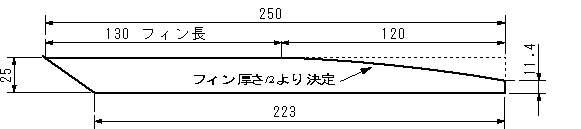 図12 側板の寸法 |
||||||
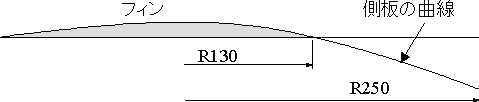 図13 側板の曲線部分の寸法 Fig.7の x=14cm〜25cmのデータ使用 |
||||||
|
●ホーン断面形状の型紙
表ホーン長xとdhの関係を図12のように、DIY店などで売られている学校教育工作用紙(いわゆるボール紙、グラフ用紙のような厚紙)にプロットして、曲線は雲形定規などでなめらかに結ぶ。
|
||||||
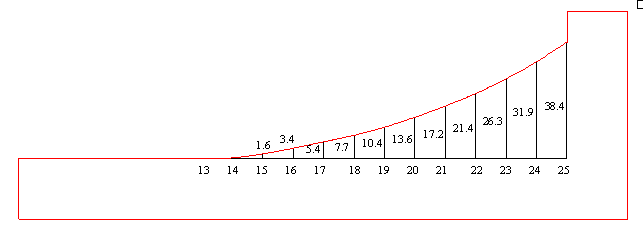 図12 ホーン部削り出しの時に使う型紙 |
||||||
|
側板のカーブ、フィンの形状の型紙も同じように作成する。
側板のカーブ ホーン長xと厚さt/2 lo<x
フィンの形状 ホーン長xと 厚さt 0≦x≦ lo
|
||||||
 B
B